
【題目】如圖,二次函數![]() 的圖象與x軸的一個交點為B(4,0),另一個交點為A,且與y軸相交于C點.
的圖象與x軸的一個交點為B(4,0),另一個交點為A,且與y軸相交于C點.
(1)求m的值及C點坐標;
(2)在直線BC上方的拋物線上是否存在一點M,使得它與B,C兩點構成的三角形面積最大,若存在,求出此時M點坐標;若不存在,請簡要說明理由;
(3)P為拋物線上一點,它關于直線BC的對稱點為Q.
①當四邊形PBQC為菱形時,求點P的坐標;
②點P的橫坐標為t(0<t<4),當t為何值時,四邊形PBQC的面積最大,請說明理由.

【答案】(1)m=4,C(0,4);(2)存在,M(2,6);(3)①P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() );②當t=2時,S四邊形PBQC最大=16.
);②當t=2時,S四邊形PBQC最大=16.
【解析】
試題分析:(1)用待定系數法求出拋物線解析式;
(2)先判斷出面積最大時,平移直線BC的直線和拋物線只有一個交點,從而求出點M坐標;
(3)①先判斷出四邊形PBQC時菱形時,點P是線段BC的垂直平分線,利用該特殊性建立方程求解;
②先求出四邊形PBCQ的面積與t的函數關系式,從而確定出它的最大值.
試題解析:(1)將B(4,0)代入![]() ,解得,m=4,∴二次函數解析式為
,解得,m=4,∴二次函數解析式為![]() ,令x=0,得y=4,∴C(0,4);
,令x=0,得y=4,∴C(0,4);
(2)存在,理由:∵B(4,0),C(0,4),∴直線BC解析式為y=﹣x+4,當直線BC向上平移b單位后和拋物線只有一個公共點時,△MBC面積最大,∴ ,∴
,∴![]() ,∴△=16﹣4b=0,∴b=4,∴
,∴△=16﹣4b=0,∴b=4,∴![]() ,∴M(2,6);
,∴M(2,6);
(3)①如圖,∵點P在拋物線上,∴設P(m,![]() ),當四邊形PBQC是菱形時,點P在線段BC的垂直平分線上,∵B(4,0),C(0,4),∴線段BC的垂直平分線的解析式為y=x,∴m=
),當四邊形PBQC是菱形時,點P在線段BC的垂直平分線上,∵B(4,0),C(0,4),∴線段BC的垂直平分線的解析式為y=x,∴m=![]() ,∴m=
,∴m=![]() ,∴P(
,∴P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() );
);
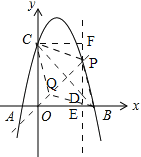
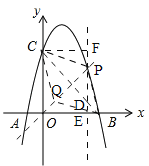
②如圖,設點P(t,![]() ),過點P作y軸的平行線l,過點C作l的垂線,∵點D在直線BC上,∴D(t,﹣t+4),∵PD=
),過點P作y軸的平行線l,過點C作l的垂線,∵點D在直線BC上,∴D(t,﹣t+4),∵PD=![]() ﹣(﹣t+4)=
﹣(﹣t+4)=![]() ,BE+CF=4,∴S四邊形PBQC=2S△PDC=2(S△PCD+S△BD)=2(
,BE+CF=4,∴S四邊形PBQC=2S△PDC=2(S△PCD+S△BD)=2(![]() PD×CF+
PD×CF+![]() PD×BE)=4PD=
PD×BE)=4PD=![]() =
=![]() ,∵0<t<4,∴當t=2時,S四邊形PBQC最大=16.
,∵0<t<4,∴當t=2時,S四邊形PBQC最大=16.


科目:初中數學 來源: 題型:
【題目】下列說法不正確的是( )
A. 零既不是正數也不是負數 B. 一個負數的絕對值是它的相反數
C. 兩個負數,絕對值大的反而小 D. 互為倒數的兩數相加得零
查看答案和解析>>
科目:初中數學 來源: 題型:
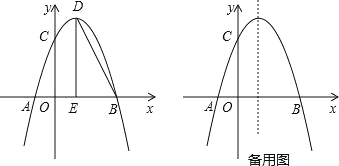
【題目】如圖,拋物線y=﹣![]() x2+bx+c與x軸交于點A,點B,與y軸交于點C,點B坐標為(6,0),點C坐標為(0,6),點D是拋物線的頂點,過點D作x軸的垂線,垂足為E,連接BD.
x2+bx+c與x軸交于點A,點B,與y軸交于點C,點B坐標為(6,0),點C坐標為(0,6),點D是拋物線的頂點,過點D作x軸的垂線,垂足為E,連接BD.
(1)求拋物線的解析式及點D的坐標;
(2)點F是拋物線上的動點,當∠FBA=∠BDE時,求點F的坐標;
(3)若點M是拋物線上的動點,過點M作MN∥x軸與拋物線交于點N,點P在x軸上,點Q在平面內,以線段MN為對角線作正方形MPNQ,請直接寫出點Q的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com