
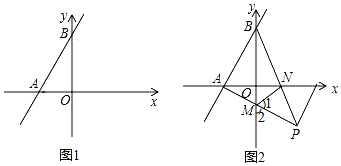
【題目】如圖1,在平面直角坐標系中,直線AB分別交x軸、y軸于點![]() 點
點![]() 且a、b滿足
且a、b滿足![]() .
.
![]() ______;
______;![]() ______.
______.
![]() 點P在直線AB的右側,且
點P在直線AB的右側,且![]() ,
,
![]() 若點P在x軸上,則點P的坐標為______;
若點P在x軸上,則點P的坐標為______;
![]() 若
若![]() 為直角三角形,求點P的坐標;
為直角三角形,求點P的坐標;
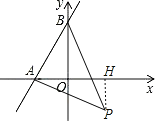
![]() 如圖2,在
如圖2,在![]() 的條件下,
的條件下,![]() 且點P在第四象限,AP與y軸交于點M,BP與x軸交于點N,連接
且點P在第四象限,AP與y軸交于點M,BP與x軸交于點N,連接![]() 求證:
求證:![]() 提示:過點P作
提示:過點P作![]() 交x軸于
交x軸于![]()
【答案】(1)![]() ,4;(2)
,4;(2)![]() ;
;![]() 或
或![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)![]() ,根據非負數的性質即可求解;
,根據非負數的性質即可求解;
(2)①點P在x軸上,則OP=OB=4,即可求解;②分∠BAP=90°、∠ABP=90°兩種情況,求解即可;
![]() 通過證明△MEP≌△HFP(AAS)得:∠2=∠FHP,證明△MNP≌△HNP(SAS),∠1=∠NHP,即可求解.
通過證明△MEP≌△HFP(AAS)得:∠2=∠FHP,證明△MNP≌△HNP(SAS),∠1=∠NHP,即可求解.
解:![]() ,
,
即:![]() ,
,![]() ,
,
故答案是![]() ,4;
,4;
![]() 點P在x軸上,則
點P在x軸上,則![]() ,
,
故:答案是![]() ;
;
![]() 當
當![]() 時,
時,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
故點P的坐標為![]() ;
;
當![]() 時,
時,
同理可得:點P的坐標為![]() ,
,
故點P的坐標為![]() 或
或![]() ;
;
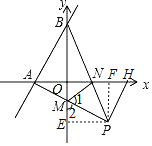
![]() 過點P作
過點P作![]() 交x軸于H,過點P分別作x、y軸的垂線,交于點F、E,
交x軸于H,過點P分別作x、y軸的垂線,交于點F、E,
由![]() 知,
知,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.
故答案為:(1)-2, 4;(2)①(4, 0);②(2,-2)或(4,2);(3)見解析.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案科目:初中數學 來源: 題型:
【題目】若三角形的一邊和該邊上的高相等的三角形稱為“和諧三角形”,如圖,已知拋物線y=ax2經過A(﹣1,1),P是y軸正半軸上的動點,射線AP與拋物線交于另一點B,當△AOP是“和諧三角形”時,點B的坐標為 . 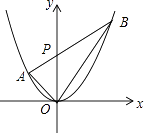
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一般地,![]() 個相同的因數
個相同的因數![]() 相乘
相乘![]() ,記為
,記為![]() , 如
, 如![]() ,此時,3叫做以2為底8的對數,記為
,此時,3叫做以2為底8的對數,記為![]() (即
(即![]() ) .一般地,若
) .一般地,若![]() 且
且![]() , 則
, 則![]() 叫做以
叫做以![]() 為底
為底![]() 的對數, 記為
的對數, 記為![]() (即
(即![]() ) .如
) .如![]() , 則4叫做以3為底81的對數, 記為
, 則4叫做以3為底81的對數, 記為![]() (即
(即![]() ) .
) .
(1)計算下列各對數的值:![]() ;
;![]() ;
;![]() .
.
(2)觀察(1)中三數4、16、64之間滿足怎樣的關系式,![]() 之間又滿足怎樣的關系式;
之間又滿足怎樣的關系式;
(3)由(2)的結果,你能歸納出一個一般性的結論嗎?
(4) 根據冪的運算法則:![]() 以及對數的含義說明上述結論.
以及對數的含義說明上述結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形![]() 是矩形,點
是矩形,點![]() 、
、![]() 在坐標軸上,
在坐標軸上, ![]() 是
是![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到的,點
得到的,點![]() 在
在![]() 軸上,直線
軸上,直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,線段
,線段![]() ,
,![]() .
.

(1)求直線![]() 的解析式;
的解析式;
(2)求![]() 的面積;
的面積;
(3)點![]() 在
在![]() 軸上,平面內是否存在點
軸上,平面內是否存在點![]() ,使以點
,使以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是矩形?若存在,請直接寫出點
為頂點的四邊形是矩形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=α.∠ABC與∠ACD的平分線交于點A1,得∠A1;∠A1BC與∠A1CD的平分線相交于點A2,得∠A2;…;∠A2019BC與∠A2019CD的平分線相交于點A2020,得∠A2020,則∠A2020=_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
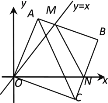
【題目】在平面直角坐標系中,邊長為3的正方形OABC的兩頂點A、C分別在y軸、x軸的正半軸上,點O在原點。現將正方形OABC繞O點順時針旋轉,當A點第一次落在直線y=x上時停止旋轉,旋轉過程中,AB邊交直線y=x于點M,BC邊交x軸于點N(如圖).在旋轉正方形OABC的過程中,△MBN的周長為________
查看答案和解析>>
科目:初中數學 來源: 題型:
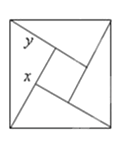
【題目】如圖所示,是用4個全等的直角三角形與1個小正方形鑲嵌而成的正方形圖案,已知大正方形面積為49,小正方形面積為4,若用x,y表示直角三角形的兩直角邊(x>y),下列四個說法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中說法正確的結論有______________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com