
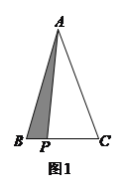
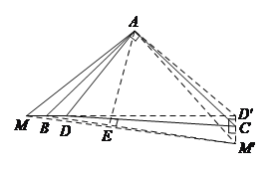
【題目】(![]() )如圖
)如圖![]() ,
,![]() 中,
中,![]() ,
,![]() 是
是![]() 上任意一點,以點
上任意一點,以點![]() 為中心,取旋轉角等于
為中心,取旋轉角等于![]() ,把
,把![]() 逆時針旋轉,畫出旋轉后的圖形.
逆時針旋轉,畫出旋轉后的圖形.
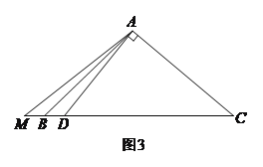
(![]() )如圖
)如圖![]() ,等邊
,等邊![]() 中,
中,![]() 為
為![]() 邊上一點,
邊上一點,![]() 在
在![]() 的延長線上,且
的延長線上,且![]() .
.
求證:![]() .
.
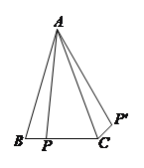
(![]() )已知:如圖
)已知:如圖![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 邊上一點,
邊上一點,![]() 為
為![]() 延長線上一點,且
延長線上一點,且![]() ,已知
,已知![]() ,
,![]() .寫出求線段
.寫出求線段![]() 長的具體思路(即添加輔助線的方法,推導的具體步驟詳寫,其它的寫出關鍵步驟或結果即可),并給出最后結果.
長的具體思路(即添加輔助線的方法,推導的具體步驟詳寫,其它的寫出關鍵步驟或結果即可),并給出最后結果.

【答案】(![]() )見解析;(
)見解析;(![]() )見解析;(
)見解析;(![]() )
)![]()
【解析】
(1)根據要求作圖即可;
(2)延長BC至點F,使CF=BD,連結EF.易證△CEF為等邊三角形,得到EF=CF,∠F=60°,從而可證△ABD≌△DFE,即可得到結論.
(3)過點C作D′ M′⊥BC,并取CD′=CM′=BD=BM.連結DD′、MM′、DM′,得到DD′=DM′,∠D′ DC=∠M′ DC,由(1)(2)可得∠D′ DC=∠BAD=7.5°,故∠CDM′=7.5°,可證得△AMM′和△ADD′為等腰直角三角形,得到AD=AD′=1,AM=AM′,DD′=![]() =DM′,∠ADD′=45°,∠ADM′=45°+7.5°+7.5°=60°.過A作AE⊥DM′于點E,得到∠DAE=30°,由30°直角三角形的性質得到DE,AE的長,進而得到EM′的長,由勾股定理即可得到結論.
=DM′,∠ADD′=45°,∠ADM′=45°+7.5°+7.5°=60°.過A作AE⊥DM′于點E,得到∠DAE=30°,由30°直角三角形的性質得到DE,AE的長,進而得到EM′的長,由勾股定理即可得到結論.
(![]() )如圖,
)如圖,![]() 即為所求,
即為所求,
(![]() )延長
)延長![]() 至點
至點![]() ,使
,使![]() ,連結
,連結![]() .
.
∵![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() 為等邊三角形.
為等邊三角形.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,得證.
,得證.
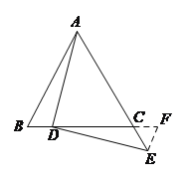
(![]() )過點
)過點![]() 作
作![]() ,并取
,并取![]() ,
,
連結![]() 、
、![]() 、
、![]() ,
,
則![]() ,
,
由(![]() )(
)(![]() )可得
)可得![]() ,
,
∴![]() ,
,
由![]() ,
,
可證得![]() ≌
≌![]() ≌
≌![]() ,
,
所以![]() 和
和![]() 為等腰直角三角形,
為等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
過![]() 作
作![]() 于點
于點![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】有理數a,b,c在數軸上的位置如圖所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”從大到小把a,b,﹣b,c連接起來.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一種密碼,將英文26個字舟a,b,c,…,z(不論大小寫)依次對應1,2,3,…,26,這26個自然數(見表格),當明碼對應的序號x為奇數時,密碼對應的序號![]() ,當明碼對應的序號x為偶數時,密碼對應的序號
,當明碼對應的序號x為偶數時,密碼對應的序號![]() +12,按下述規定,將明碼“love”譯成密碼是( )
+12,按下述規定,將明碼“love”譯成密碼是( )

A.loveB.rkwuC.sdriD.rewj
查看答案和解析>>
科目:初中數學 來源: 題型:
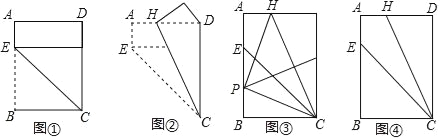
【題目】對給定的一張矩形紙片ABCD進行如下操作:先沿CE折疊,使點B落在CD邊上(如圖①),再沿CH折疊,這時發現點E恰好與點D重合(如圖②)
(1)根據以上操作和發現,求![]() 的值;
的值;
(2)將該矩形紙片展開.
①如圖③,折疊該矩形紙片,使點C與點H重合,折痕與AB相交于點P,再將該矩形紙片展開.求證:∠HPC=90°;
②不借助工具,利用圖④探索一種新的折疊方法,找出與圖③中位置相同的P點,要求只有一條折痕,且點P在折痕上,請簡要說明折疊方法.(不需說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】西安市管理部門對“十一”國慶放假期間七天本市某景區客流變化量進行了不完全統計,數據如下(用正數表示客流量比前一天增加,用負數表示客流量比前一天下降):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
變化(萬人) |
|
|
|
|
|
|
|
請通過計算解決以下問題:
(1)請判斷這7天中,哪一天人數最多?哪一天人數最少?
(2)與10月3日相比,10月5日的客流量是上升了還是下降了?
(3)如圖9月30日的客流量為1.5萬人,據統計平均每人每天消費200元,請問該景區在“十一”七天國慶假期的總收入為多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機小張某天上午營運全是在東西走向的政府大道上進行的,如果規定向東為正,向西為負,他這天上午的行程是(單位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)將最后一名乘客送達目的地時,小張距上午出發點的距離是多少千米?在出發點的什么方向?
(2)若汽車耗油量為0.6升/千米,出車時,郵箱有油72.2升,若小張將最后一名乘客送達目的地,再返回出發地,問小張今天上午是否需要加油?若要加油至少需要加多少才能返回出發地?若不用加油,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知點M,N的坐標分別為(﹣1,2),(2,1),若拋物線y=ax2﹣x+2(a≠0)與線段MN有兩個不同的交點,則a的取值范圍是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
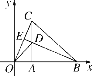
【題目】如圖,在平面直角坐標系中,等腰△OBC的邊OB在x軸上,OB=CB,OB邊上的高CA與OC邊上的高BE相交于點D,連接OD,AB=![]() ,∠CBO=45°,在直線BE上求點M,使△BMC與△ODC相似,則點M的坐標是________.
,∠CBO=45°,在直線BE上求點M,使△BMC與△ODC相似,則點M的坐標是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
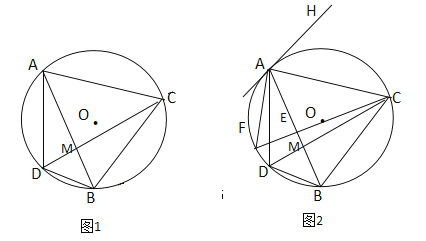
【題目】如圖1,已知⊙O是ΔADB的外接圓,∠ADB的平分線DC交AB于點M,交⊙O于點C,連接AC,BC.
(1)求證:AC=BC;
(2)如圖2,在圖1 的基礎上做⊙O的直徑CF交AB于點E,連接AF,過點A作⊙O的切線AH,若AH//BC,求∠ACF的度數;
(3)在(2)的條件下,若ΔABD的面積為![]() ,ΔABD與ΔABC的面積比為2:9,求CD的長.
,ΔABD與ΔABC的面積比為2:9,求CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com