【題目】中國科學技術館有“圓與非圓”展品，涉及了“等寬曲線”的知識．因為圓的任何一對平行切線的距離總是相等的，所以圓是“等寬曲線”．除了例以外，還有一些幾何圖形也是“等寬曲線”，如勒洛只角形(圖1)，它是分別以等邊三角形的征個頂點為圓心，以邊長為半徑，在另兩個頂點間畫一段圓弧．三段圓弧圍成的曲邊三角形．圖2是等寬的勒洛三角形和圓．
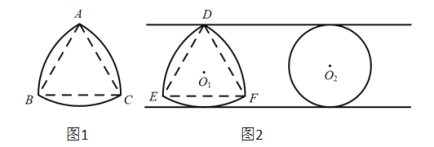
下列說法中錯誤的是( )
A.勒洛三角形是軸對稱圖形
B.圖1中，點A到
上任意一點的距離都相等
C.圖2中，勒洛三角形上任意一點到等邊三角形DEF的中心
的距離都相等
D.圖2中，勒洛三角形的周長與圓的周長相等
科目：初中數學 來源： 題型：
【題目】如圖1，在矩形
中，
是
上一點，點
從點
沿折線
運動到點
時停止；點
從點沿
運動到點時停止，速度均為每秒1個單位長度．如果點，同時開始運動，設運動時間為
，
的面積為
，已知與的函數圖象如圖2所示，有以下結論：
①
；
②
；
③當
時，
；
④當
時，是等腰三角形；
⑤當
時，
．
其中正確的有（ ）．
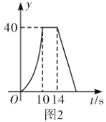
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，直線
與
軸交于點
與
軸交于點
二次函數
的圖象經過
兩點，且與軸的負半軸交于點
．
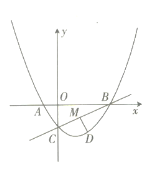
求二次函數的解析式及點的坐標．
點
是線段
上的一動點，動點
在直線下方的二次函數圖象上．設點的橫坐標為
．過點作
于點
求線段
的長關于的函數解析式，并求線段的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：有一組鄰邊相等，并且它們的夾角是直角的凸四邊形叫做等腰直角四邊形．
（1）如圖1，等腰直角四邊形ABCD，AB=BC，∠ABC=90°．
①若AB=CD=1，AB∥CD，求對角線BD的長．
②若AC⊥BD，求證：AD=CD；
（2）如圖2，在矩形ABCD中，AB=5，BC=9，點P是對角線BD上一點，且BP=2PD，過點P作直線分別交邊AD，BC于點E，F，使四邊形ABFE是等腰直角四邊形，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“校園安全”受到全社會的廣泛關注，我市某中學對部分學生就校園安全知識的了解程度，采用隨機抽樣調查的方式，并根據收集到的信息進行統計，繪制了下面兩幅尚不完整的統計圖．請你根據統計圖中所提供的信息解答下列問題：
(1)接受問卷調查的學生共有_______人，扇形統計圖中“基本了解”部分所對應扇形的圓心角為_______°；
(2)請補全條形統計圖；
(3)若該中學共有學生1800人，請根據上述調查結果，估計該中學學生中對校園安全知識 達到“了解”和“基本了解”程度的總人數；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】昆明市某中學“綜合實踐活動”棋類社團前兩次購買的兩種材質的圍棋采購如表（近期兩種材質的圍棋的售價一直不變）：
塑料圍棋 | 玻璃圍棋 | 總價（元） | |
第一次（盒） |
|
|
|
第二次（盒） |
|
|
|
（1）若該社團計劃再采購這兩種材質的圍棋各
盒，則需要多少元；
（2）若該社團準備購買這兩種材質的圍棋共
盒，且要求塑料圍棋的數量不多于玻璃圍棋數量的
倍，請設計出最省錢的購買方案，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
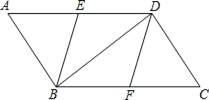
【題目】如圖，在ABCD中，點E、F分別是AD、BC的中點，分別連接BE、DF、BD．
（1）求證：△AEB≌△CFD；
（2）若四邊形EBFD是菱形，求∠ABD的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
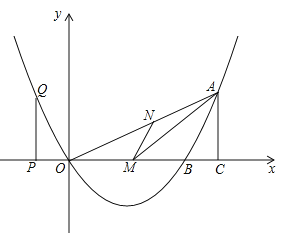
【題目】如圖，已知二次函數的圖象過點
．
，與
軸交于另一點
，且對稱軸是直線
．
（1）求該二次函數的解析式；
（2）若
是
上的一點，作
交
于
，當
面積最大時，求
的長；
（3）
是軸上的點，過作
軸與拋物線交于
，過
作
軸于
，當以
為頂點的三角形與以
為頂點的三角形相似時，求點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y=mx+n與雙曲線y=
相交于A（﹣1，2）、B（2，b）兩點，與y軸相交于點C．
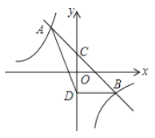
（1）求m，n的值；
（2）若點D與點C關于x軸對稱，求△ABD的面積；
（3）在坐標軸上是否存在異于D點的點P，使得S△PAB=S△DAB？若存在，直接寫出P點坐標；若不存在，說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
