【題目】如圖，利用一面墻(墻的長度不超過45m)，用80m長的籬笆圍一個矩形場地．
(1)怎樣圍才能使矩形場地的面積為750m2？
(2)能否使所圍矩形場地的面積為810m2 ，為什么？
【答案】（1）當所圍矩形的長為30m、寬為25m時，能使矩形的面積為750m2（2）不能
【解析】試題分析：（1）設所圍矩形ABCD的長AB為x米，則寬AD為
（80-x）米，根據矩形面積的計算方法列出方程求解；
（2）假使矩形面積為810，則x無實數根，所以不能圍成矩形場地．
試題解析：解：（1）設所圍矩形ABCD的長AB為x米，則寬AD為
（80-x）米．
依題意，得x（80-x）=750，即，x2-80x+1500=0，
解此方程，得x1=30，x2=50．
∵墻的長度不超過45m，∴x2=50不合題意，應舍去（4分）．
當x=30時，（80-x）=
×（80-30）=25，
所以，當所圍矩形的長為30m、寬為25m時，能使矩形的面積為750m2；
（2）不能．
因為由x
（80-x）=810得x2-80x+1620=0，
又∵b2-4ac=（-80）2-4×1×1620=-80＜0，
∴上述方程沒有實數根．
因此，不能使所圍矩形場地的面積為810m2．
科目：初中數學 來源： 題型：
【題目】如圖，O是坐標原點，直線OA與雙曲線
在第一象限內交于點A，過點A作AB⊥x軸，垂足為B，若OB=4，tan∠AOB=
．
（1）求雙曲線的解析式；
（2）直線AC與y軸交于點C（0，1），與x軸交于點D，求D點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市政府大力扶持大學生創業．李明在政府的扶持下投資銷售一種進價為每件20元的護眼臺燈．銷售過程中發現，每月銷售量y（件）與銷售單價x（元）之間的關系可近似的看作一次函數： 
．
（1）設李明每月獲得利潤為w（元），當銷售單價定為多少元時，每月可獲得最大利潤？
（2）如果李明想要每月獲得2000元的利潤，那么銷售單價應定為多少元？
（3）根據物價部門規定，這種護眼臺燈的銷售單價不得高于32元，如果李明想要每月獲得的利潤不低于2000元，那么他每月的成本最少需要多少元？（成本＝進價×銷售量）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某縣舉辦老、中、青三個年齡段五公里競走活動，其人數比為
，如圖所示的扇形統計圖表示 上述分布情況，已知老人有
人，則下列說法不正確的是（ ）
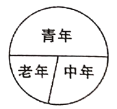
A. 老年所占區域的圓心角是
B. 參加活動的總人數是
人
C. 中年人比老年人多
D. 老年人比青年人少人
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,在平面直角坐標系中,動點P按圖中箭頭所示方向從原點出發,第1次運動到P1(1,1),第2次接著運動到點P2(2，0)，第3次接著運動到點P3(3，-2)，…，按這的運動規律,點P2019的坐標是_____.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果二次函數的二次項系數為1，那么此二次函數可表示為y＝x2＋px＋q，我們稱[p，q]為此函數的特征數，如函數y＝x2＋2x＋3的特征數是[2，3]．
(1)若一個函數的特征數為[－2，1]，求此函數圖象的頂點坐標；
(2)探究下列問題：
①若一個函數的特征數為[4，－1]，將此函數的圖象先向右平移1個單位長度，再向上平移1個單位長度，求得到的圖象對應的函數的特征數；
②若一個函數的特征數為[2，3]，問此函數的圖象經過怎樣的平移，才能使得到的圖象對應的函數的特征數為[3，4]?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
