
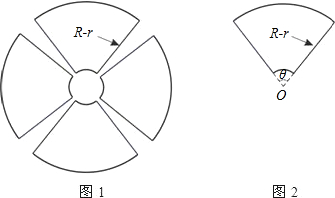
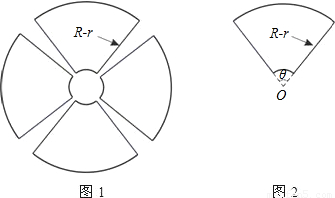
一園林設計師要使用長度為4L的材料建造如圖1所示的花圃,該花圃是由四個形狀、大小完全一樣的扇環面組成,每個扇環面如圖2所示,它是以點O為圓心的兩個同心圓弧和延長后通過O點的兩條直線段圍成,為使得綠化效果最佳,還須使得扇環面積最大.

(1)求使圖1花圃面積為最大時R-r的值及此時花圃面積,其中R、r分別為大圓和小圓的半徑;
(2)若L=160m,r=10m,求使圖2面積為最大時的θ值.
(1)花圃面積最大時 的值為
的值為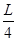 ,最大面積為
,最大面積為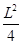 (2)
(2)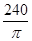 度
度
【解析】解:(1)若使形如圖1花圃面積為最大,則必定要求圖2扇環面積最大.
設圖2扇環的圓心角為θ,面積為S,根據題意得:
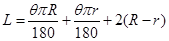 ,
………………………2分
,
………………………2分
= .
.
∴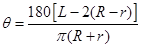 .
……………………………3分
.
……………………………3分
∴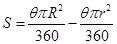 =
=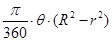 ……………………………4分
……………………………4分
=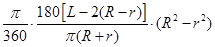
=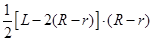 =
=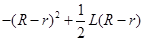
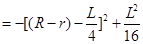
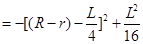 .
……………………………5分
.
……………………………5分
∵式中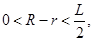 ∴S在
∴S在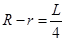 時為最大,最大值為
時為最大,最大值為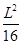 . ………6分
. ………6分
∴花圃面積最大時 的值為
的值為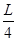 ,最大面積為
,最大面積為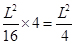 . ……………7分
. ……………7分
(2)∵當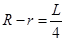 時,S取值最大,
時,S取值最大,
∴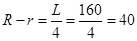 (m),
(m),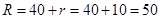 (m). …………………………8分
(m). …………………………8分
∴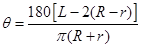 =
=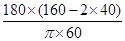 =
=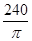 (度). ………………………10分
(度). ………………………10分
(1)由于花圃是由四個形狀、大小完全一樣的扇環面組成,則圖1 一個扇環的周長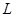 等于兩個扇形的弧長與兩個
等于兩個扇形的弧長與兩個 的和,根據弧長公式得到
的和,根據弧長公式得到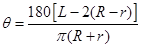 ,再根據扇形面積公式,化簡得
,再根據扇形面積公式,化簡得
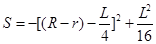 ,根據二次函數的最值即可解決問題
,根據二次函數的最值即可解決問題
(2)根據(1)中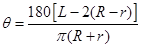 ,可以求出
,可以求出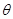 值
值


科目:初中數學 來源: 題型:
 其中R、r分別為大圓和小圓的半徑;
其中R、r分別為大圓和小圓的半徑;查看答案和解析>>
科目:初中數學 來源:2007年初中畢業升學考試(安徽蕪湖卷)數學(帶解析) 題型:解答題
一園林設計師要使用長度為4L的材料建造如圖1所示的花圃,該花圃是由四個形狀、大小完全一樣的扇環面組成,每個扇環面如圖2所示,它是以點O為圓心的兩個同心圓弧和延長后通過O點的兩條直線段圍成,為使得綠化效果最佳,還須使得扇環面積最大.
(1)求使圖1花圃面積為最大時R-r的值及此時花圃面積,其中R、r分別為大圓和小圓的半徑;
(2)若L=160m,r=10m,求使圖2面積為最大時的θ值.
查看答案和解析>>
科目:初中數學 來源:第28章《圓》中考題集(77):28.3 圓中的計算問題(解析版) 題型:解答題
 其中R、r分別為大圓和小圓的半徑;
其中R、r分別為大圓和小圓的半徑;查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《圓》(10)(解析版) 題型:解答題
 其中R、r分別為大圓和小圓的半徑;
其中R、r分別為大圓和小圓的半徑;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com