
【題目】如圖,已知直線y=![]() x+2交x軸于點A,交y軸于點B,
x+2交x軸于點A,交y軸于點B,
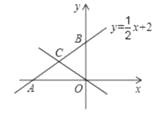
(1)求A,B兩點的坐標;
(2)已知點C是線段AB上的一點,當S△AOC= ![]() S△AOB時,求直線OC的解析式。
S△AOB時,求直線OC的解析式。
【答案】(1)點A的坐標為(-4,0),點B的坐標為(0,2);(2)y=-![]() x
x
【解析】
(1)分別令y=0, x=0, 代入一次函數式,即可求出A、B點的坐標;
(2)先由OA和OB的長求出△AOB的面積,設C點坐標為(m,n),△AOC和△AOB等底不同高, 由 S△AOC=![]() S△AOB列式,求出C點的縱坐標n,把n代入一次函數式求出m, 從而得出C點坐標, 設直線OC的解析式為y=kx,根據C點坐標用待定系數法求出k, 即可確定直線OC的函數解析式.
S△AOB列式,求出C點的縱坐標n,把n代入一次函數式求出m, 從而得出C點坐標, 設直線OC的解析式為y=kx,根據C點坐標用待定系數法求出k, 即可確定直線OC的函數解析式.
(1)解:∵直線y= ![]() x+2,
x+2,
∴當x=0時,y=2,當y=0時,x=-4
∵直線y= ![]() x+2交x軸于點A,交y軸于點B,
x+2交x軸于點A,交y軸于點B,
∴點A的坐標為(-4,0),點B的坐標為(0,2)
(2)解:由(1)知,點A的坐標為(-4,0),點B的坐標為(0,2),
∴OA=4,OB=2,
∴S△AOB= ![]() =4
=4
S△AOC= ![]() S△AOB ,
S△AOB ,
∴S△AOC=2
設點C的坐標為(m,n)
∴ ![]() =2,得n=1,
=2,得n=1,
∵點C在線段AB上,
∴1= ![]() m+2,得m=-2
m+2,得m=-2
∴點C的坐標為(-2,1)
設直線OC的解析式為y=kx
-2k=1,得k=- ![]() ,
,
即直線OC的函數解析式為y=-![]() x
x


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=24厘米,BC=16厘米,點D為AB的中點,點P在線段BC上以4厘米/秒的速度由B點向C點運動,同時,點Q在線段CA上由C點向A點運動.當點Q的運動速度為_______厘米/秒時,能夠在某一時刻使△BPD與△CQP全等.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店出售網球和網球拍,網球拍每只定價80元,網球每個定價4元,商家為促銷商品,同時向客戶提供兩種優惠方案:①買一只網球拍送3個網球:②網球拍和網球都按定價的9折優惠,現在某客戶要到該商店購買球拍20只,網球![]() 個(
個(![]() 大于20).
大于20).
(1)若該客戶按優惠方案①購買需付款多少元?(用含![]() 的式子表示)
的式子表示)
(2)若該客戶按優惠方案②購買需付款多少元?(用含![]() 的式子表示)
的式子表示)
(3)若![]() 時,通過計算說明,此時按哪種優惠方案購買較為合算?
時,通過計算說明,此時按哪種優惠方案購買較為合算?
(4)當![]() 時,你能結合兩種優惠方案給出一種更為省錢的購買方案嗎?試寫出你的購買方案,并計算出所需的錢數.
時,你能結合兩種優惠方案給出一種更為省錢的購買方案嗎?試寫出你的購買方案,并計算出所需的錢數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為選拔參加全市中學生數學競賽的學生,八(2)班組織了一次班內數學競賽活動,競賽活動分小組進行,其中甲、乙兩組各5人的成績如下圖所示(120分制).

(1)填寫下表:
平均數 | 中位數 | |
甲 | ________ | 90 |
乙 | 90 | ________ |
(2)請計算甲、乙兩組競賽成績的方差,并說明在這次數學競賽中,哪一組的成績更為穩定?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明從家出發,外出散步,到一個公共閱報欄前看了一會報后,繼續散步了一段時間,然后回家,如圖描述了小明在散步過程匯總離家的距離s(米)與散步所用時間t(分)之間的函數關系,根據圖象,下列信息錯誤的是( )

A.小明看報用時8分鐘
B.公共閱報欄距小明家200米
C.小明離家最遠的距離為400米
D.小明從出發到回家共用時16分鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線CB∥OA,∠C=∠OAB=120°,E、F在CB上,且滿足∠FOB=∠AOB,OE平分∠COF.

(1)求∠EOB的度數.
(2)若平行移動AB,那么∠OBC:∠OFC的值是否隨之發生變化? 若變化,找出變化規律或求出變化范圍;若不變,求出這個比值.
(3)在平行移動AB的過程中,是否存在某種情況,使∠OEC=∠OBA? 若存在,求出∠OBA的度數;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了解該校學生的體育鍛煉情況,隨機抽查了該校部分學生一周的體育鍛煉時間的情況,并繪制了如下兩幅不完整的統計圖:
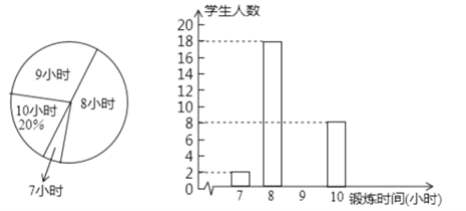
根據以上信息解答以下問題:
(1)本次抽查的學生共有多少名,并補全條形統計圖;
(2)寫出被抽查學生的體育鍛煉時間的眾數和中位數;
(3)該校一共有1800名學生,請估計該校學生一周體育鍛煉時間不低于9小時的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4張相同的卡片上分別寫有數字-1、-3、4、6,將卡片的背面朝上,并洗勻.
(1)從中任意抽取1張,抽到的數字是奇數的概率是 ;
(2)從中任意抽取1張,并將所取卡片上的數字記作一次函數![]() 中的
中的![]() ;再從余下的卡片中任意抽取1張,并將所取卡片上的數字記作一次函數
;再從余下的卡片中任意抽取1張,并將所取卡片上的數字記作一次函數![]() 中的
中的![]() .利用畫樹狀圖或列表的方法,求這個一次函數的圖象經過第一、二、四象限的概率.
.利用畫樹狀圖或列表的方法,求這個一次函數的圖象經過第一、二、四象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為了鼓勵居民節約用水,決定實行兩級收費制度.若每月用水量不超過14噸(含14噸),則每噸按政府補貼優惠價m元收費;若每月用水量超過14噸,則超過部分每噸按市場價n元收費.小明家3月份用水20噸,交水費49元;4月份用水18噸,交水費42元.
(1)求每噸水的政府補貼優惠價和市場價分別是多少?
(2)小明家5月份用水26噸,則他家應交水費多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com