
【題目】“分塊計數法”:對有規律的圖形進行計數時,有些題可以采用“分塊計數”的方法.
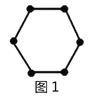
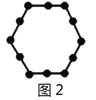
例如:圖1有6個點,圖2有12個點,圖3有18個點,…,按此規律,求圖8、圖![]() 有多少個點?
有多少個點?
我們將每個圖形分成完全相同的6塊,每塊黑點的個數相同(如圖),這樣圖1中黑點個數是![]() 個;圖2中黑點個數是
個;圖2中黑點個數是![]() 個;圖3中黑點個數是
個;圖3中黑點個數是![]() 個;…,所以容易求出圖8、圖
個;…,所以容易求出圖8、圖![]() 中黑點的個數分別是______、_________.
中黑點的個數分別是______、_________.

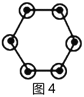
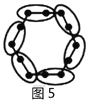
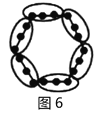
請你參考以上“分塊計數法”,先將下面的點陣進行分塊(畫在答題卡上),再完成以下問題:
(1)第6個點陣中有______個圓圈;第![]() 個點陣中有______個圓圈.
個點陣中有______個圓圈.
(2)小圓圈的個數會等于331嗎?請求出是第幾個點陣.


【答案】48;6n;(1)91;![]() ;(2)會;第11個點陣
;(2)會;第11個點陣
【解析】
根據規律可求得圖8中黑點個數和圖n中黑點個數;
(1)第2個圖中2為一塊,分為3塊,余1,第3個圖中3為一塊,分為6塊,余1;按此規律得:第6個點陣中6為一塊,分為15塊,余1,得第n個點陣中有:n×3(n-1)+1=3n2-3n+1;
(2)令3n2-3n+1=331,方程有解則存在這樣的點陣,據此解答.
解:圖8中黑點個數是6×8=48個;圖n中黑點個數是6n個;
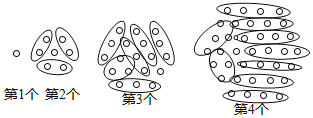
(1)如圖所示:第1個點陣中有:1個,
第2個點陣中有:2×3+1=7個,
第3個點陣中有:3×6+1=19個,
第4個點陣中有:4×9+1=37個,
第5個點陣中有:5×12+1=61個,
第6個點陣中有:6×15+1=91個,
…
第n個點陣中有:n×3(n-1)+1=3n2-3n+1,
故答案為:91,3n2-3n+1;
(2)3n2-3n+1=331,
n2-n-110=0,
(n-11)(n+10)=0,
n1=11,n2=-10(舍),
∴小圓圈的個數會等于331,它是第11個點陣.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:
【題目】快遞公司為提高快遞分揀的速度,決定購買機器人來代替人工分揀,兩種型號的機器人的工作效率和價格如表:
型號 | 甲 | 乙 |
每臺每小時分揀快遞件數(件) | 1000 | 800 |
每臺價格(萬元) | 5 | 3 |
該公司計劃購買這兩種型號的機器人共10臺,并且使這10臺機器人每小時分揀快遞件數總和不少于8500件
(1)設購買甲種型號的機器人x臺,購買這10臺機器人所花的費用為y萬元,求y與x之間的關系式;
(2)購買幾臺甲種型號的機器人,能使購買這10臺機器人所花總費用最少?最少費用是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某品牌電腦銷售公司有營銷員14人,銷售部為制定營銷人員月銷售電腦定額,統計了這14人某月的銷售量如下(單位:臺):
銷售量 | 200 | 170 | 130 | 80 | 50 | 40 |
人數 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)該公司營銷員銷售該品牌電腦的月銷售平均數是 臺,中位數是 臺,眾數是 臺.
(2)銷售部經理把每位營銷員月銷售量定為90臺,你認為是否合理?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題)若a+b=10,則ab的最大值是多少?
(探究)
探究一:當a﹣b=0時,求ab值.
顯然此時,a=b=5,則ab=5×5=25
探究二:當a﹣b=±1時,求ab值.
①a﹣b=1,則a=b+1,
由已知得b+1+b=10
解得 b=![]() ,
,
a=b+l=![]() +1=
+1=![]()
則ab=![]() =
=![]()
②a﹣b=﹣1,即b﹣a=1,由①可得,b=![]() ,a=
,a=![]()
則ab=![]() =
=![]() .
.
探究三:當a﹣b=±2時,求ab值(仿照上述方法,寫出探究過程).
探究四:完成下表:
a﹣b | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
ab | … |
|
|
| 25 |
|
|
| … |
(結論)若a+b=10,則ab的最大值是 (觀察上面表格,直接寫出結果).
(拓展)若a+b=m,則ab的最大值是 .
(應用)用一根長為12m的鐵絲圍成一個長方形,這個長方形面積的最大值是 m2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上的A、B、C三點所表示的數分別為a、b、1,且|a﹣1|+|b﹣1|=|a﹣b|,則下列選項中,滿足A、B、C三點位置關系的數軸為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
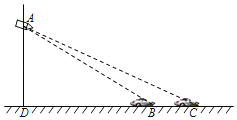
【題目】如圖,一輛轎車在經過某路口的感應線B和C處時,懸臂燈桿上的電子警察拍攝到兩張照片,兩感應線之間距離BC為6m,在感應線B、C兩處測得電子警察A的仰角分別為∠ABD=18°,∠ACD=14°.求電子警察安裝在懸臂燈桿上的高度AD的長.
(參考數據:sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
查看答案和解析>>
科目:初中數學 來源: 題型:
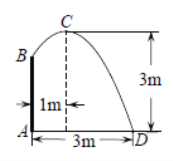
【題目】如圖,在噴水池的中心![]() 處豎直安裝一根水管
處豎直安裝一根水管![]() ,水管的頂端安有一個噴水頭,使噴出的拋物線形水柱在與池中心
,水管的頂端安有一個噴水頭,使噴出的拋物線形水柱在與池中心![]() 的水平距離為1m處達到最高點
的水平距離為1m處達到最高點![]() ,高度為3m,水柱落地點
,高度為3m,水柱落地點![]() 離池中心
離池中心![]() 處3m,以水平方向為
處3m,以水平方向為![]() 軸,建立平面直角坐標系,若選取點
軸,建立平面直角坐標系,若選取點![]() 為坐標原點時的拋物線的表達式為
為坐標原點時的拋物線的表達式為![]() ,則選取點
,則選取點![]() 為坐標原點時的拋物線表達式為______,其中自變量的取值范圍是______,水管
為坐標原點時的拋物線表達式為______,其中自變量的取值范圍是______,水管![]() 的長為______m.
的長為______m.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com