
【題目】如圖1,在直角坐標系xOy中,點A在y軸上,點B,點C在x軸上,點C在點B的右側,OA=2OB=2BC=2.
(1)點C的坐標是 ;
(2)點P是x軸上一點,點P到AC的距離等于AC的長度,求點P的坐標;
(3)如圖2,點D是AC上一點,∠CBD=∠ABO,連接OD,在AB上是否存在一點Q,使QB=AB﹣OD,若存在,求點Q與點D的橫坐標之和,若不存在,請說明理由.

【答案】(1)(2,0);(2)P(﹣2,0)或(6,0);(3)點Q與點D的橫坐標之和為2或![]() .
.
【解析】
(1)根據2OB=2BC=2,可得OB=BC=1,進而可求得OC=OB+BC=2,所以C(2,0),
(2)如圖1,
根據OA=2,可得A(0,2),根據C(2,0)由勾股定理可得:AC=2![]() ,
,
過點P作PD⊥AC于D,根據點P到AC的距離等于AC的長度,可得DP=AC=2![]() ,
,
再根據∠PDC=∠AOC,∠PCD=∠ACO,可證:△PCD∽△ACO,根據相似三角形的性質可得:
![]() 即
即![]() ,解得PC=4,進而求得:OP=PC+OC=4+2=6,所以P(6,0)或OP=PC﹣OC=4﹣2=2,即:P(﹣2,0)或(6,0),
,解得PC=4,進而求得:OP=PC+OC=4+2=6,所以P(6,0)或OP=PC﹣OC=4﹣2=2,即:P(﹣2,0)或(6,0),
(3)如圖2,延長DB交y軸點E,可得∠DBC=∠OBE,
根據∠DBC=∠ABO,可得:∠OBC=∠OBA,根據OB⊥AE,可得OE=OA=2,求得E(0,﹣2),
根據OB=1,可得B(1,0),利用待定系數法求得:直線BD的解析式為y=2x﹣2①,
再根據A(0,2),C(2,0),可求得直線AC的解析式為y=﹣x+2②,聯立①②解得,x=![]() ,y=
,y=![]() ,
,
求出點D(![]() ,
,![]() ),故OD=
),故OD=![]() ,根據A(0,2),B(1,0),可得直線AB的解析式為y=﹣2x+2,
,根據A(0,2),B(1,0),可得直線AB的解析式為y=﹣2x+2,
設點Q(m,﹣2m+2),由B(1,0),利用勾股定理可得:BQ=![]() =
=![]() |m﹣1|,由A(0,2),B(1,0),可求得:AB=
|m﹣1|,由A(0,2),B(1,0),可求得:AB=![]() ,再根據QB=AB﹣OD,可得
,再根據QB=AB﹣OD,可得![]() |m﹣1|=
|m﹣1|=![]() ﹣
﹣![]() =
=![]() ,
,
解得:m=![]() 或m=
或m=![]() ,進而可得:Q(
,進而可得:Q(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),所以點Q與點D的橫坐標之和為
),所以點Q與點D的橫坐標之和為![]() +
+![]() =2或
=2或![]() +
+![]() =
=![]() .
.
解:(1)∵2OB=2BC=2,
∴OB=BC=1,
∴OC=OB+BC=2,
∴C(2,0),
故答案為:(2,0),
(2)如圖1,
∵OA=2,
∴A(0,2),
∵C(2,0),
∴AC=2![]() ,
,
過點P作PD⊥AC于D,
∵點P到AC的距離等于AC的長度,
∴DP=AC=2![]() ,
,
∵∠PDC=∠AOC,∠PCD=∠ACO,
∴△PCD∽△ACO,
∴![]() ,
,
∴![]()
∴PC=4,
∴OP=PC+OC=4+2=6,
∴P(6,0)或OP=PC﹣OC=4﹣2=2,
∴P(﹣2,0),
即:P(﹣2,0)或(6,0),
(3)存在,理由:如圖2,
延長DB交y軸點E,
∴∠DBC=∠OBE,
∵∠DBC=∠ABO,
∴∠OBC=∠OBA,
∵OB⊥AE,
∴OE=OA=2,
∴E(0,﹣2),
∵OB=1,
∴B(1,0),
∴直線BD的解析式為y=2x﹣2①,
∵A(0,2),C(2,0),
∴直線AC的解析式為y=﹣x+2②,
聯立①②解得,x=![]() ,y=
,y=![]() ,
,
∴D(![]() ,
,![]() ),
),
∴OD=![]() ,
,
∵A(0,2),B(1,0),
∴直線AB的解析式為y=﹣2x+2,
設點Q(m,﹣2m+2),
∵B(1,0),
∴BQ=![]() =
=![]() |m﹣1|,
|m﹣1|,
∵A(0,2),B(1,0),
∴AB=![]() ,
,
∵QB=AB﹣OD,
∴![]() |m﹣1|=
|m﹣1|=![]() ﹣
﹣![]() =
=![]() ,
,
∴m=![]() 或m=
或m=![]() ,
,
∴Q(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ),
),
∴點Q與點D的橫坐標之和為![]() +
+![]() =2或
=2或![]() +
+![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】圓桌面(桌面中間有一個直徑為0.4m的圓洞)正上方的燈泡(看作一個點)發出的光線照射平行于地面的桌面后,在地面上形成如圖所示的圓環形陰影.已知桌面直徑為1.2m,桌面離地面1m,若燈泡離地面3m,則地面圓環形陰影的面積是( ) 
A.0.324πm2
B.0.288πm2
C.1.08πm2
D.0.72πm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等.經洽談,甲商場的優惠方案是:每購買10套隊服,送1個足球;乙商場的優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)每套隊服和每個足球的價格分別是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所需的費用.
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是⊙O的內接三角形,AB為直徑,過點B的切線與AC的延長線交于點D,E是BD中點,連接CE.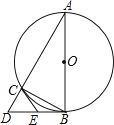
(1)求證:CE是⊙O的切線;
(2)若AC=4,BC=2,求BD和CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在2016CCTV英語風采大賽中,婁底市參賽選手表現突出,成績均不低于60分.為了更好地了解婁底賽區的成績分布情況,隨機抽取利了其中200名學生的成績(成績x取整數,總分100分)作為樣本進行了整理,得到如圖的兩幅不完整的統計圖表:
根據所給信息,解答下列問題: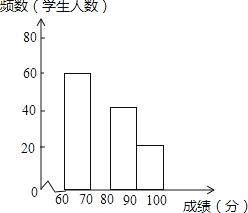
(1)在表中的頻數分布表中,m= , n= .
成績 | 頻數 | 頻率 |
60≤x<70 | 60 | 0.30 |
70≤x<80 | m | 0.40 |
80≤x<90 | 40 | n |
90≤x≤100 | 20 | 0.10 |
(2)請補全圖中的頻數分布直方圖.
(3)按規定,成績在80分以上(包括80分)的選手進入決賽.若婁底市共有4000人參數,請估計約有多少人進入決賽?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a、b、c為常數,a≠0)經過點A(﹣1,0),B(5,﹣6),C(6,0).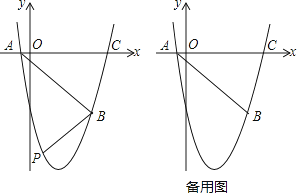
(1)求拋物線的解析式;
(2)如圖,在直線AB下方的拋物線上是否存在點P使四邊形PACB的面積最大?若存在,請求出點P的坐標;若不存在,請說明理由;
(3)若點Q為拋物線的對稱軸上的一個動點,試指出△QAB為等腰三角形的點Q一共有幾個?并請求出其中某一個點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】填空并解答:
規定:a2=a×a,a3=a×a×a,an=a×a×…×a(n 個 a)
(1)(2×3)2= ,22×32= ,你發現(2× 3)2 的值與 22×32 的值 .
(2)(2×3)3= ,23×33= ,你發現(2×3)3 的值與 23×33 的值 .
由此,我們可以猜想:(a×b)2 a2×b2,(a×b)3 a3×b3,…(a×b)n an×bn.
(3)利用(2)題結論計算(﹣2)2018×(﹣![]() )2019 的值.
)2019 的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com