
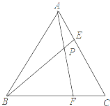
【題目】如圖,等邊三角形ABC的邊長為![]() cm,在AC,BC邊上各取一點E,F,使得AE=CF,連接AF,BE相交于點P.(1)則∠APB=______度;(2)當點E從點A運動到點C時,則動點P經過的路徑長為________cm.
cm,在AC,BC邊上各取一點E,F,使得AE=CF,連接AF,BE相交于點P.(1)則∠APB=______度;(2)當點E從點A運動到點C時,則動點P經過的路徑長為________cm.
【答案】120 ![]()
【解析】
(1)證明△ABE≌△CAF,借用外角即可以得到答案;
(2)由∠APB=120°可知點P的運動路徑是一段弧,根據圓周角定理可得∠AOB=120°,過圓心O做OG⊥AB,由AB=![]() 可得OA=1,然后利用弧長公式計算即可.
可得OA=1,然后利用弧長公式計算即可.
解:(1)∵△ABC為等邊三角形,
∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
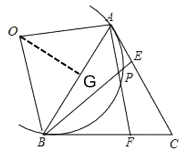
在△ABE和△CAF中,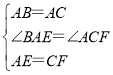 ,
,
∴△ABE≌△CAF(SAS),
∴∠ABE=∠CAF,
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°,
∴∠APB=180°∠APE=120°;
(2)由∠APB=120°可知點P的運動路徑是一段弧,如圖,
∵∠APB=120°,
所以劣弧AB所對的圓周角為60°,
∴∠AOB=120°,
過圓心O做OG⊥AB,則∠AOG=30°,
又∵AB=![]() ,
,
∴AG=![]() ,
,
∴OA=![]() ,
,
∴動點P經過的路徑長l=![]() .
.
故答案為:(1)120;(2)![]() .
.


 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2﹣2(a+1)x+a2+3=0有兩個實數根x1,x2
(1)求實數a的取值范圍
(2)若等腰△ABC的三邊長分別為x1,x2,6,求△ABC的周長
(3)是否存在實數a,使x1,x2恰是一個邊長為![]() 的菱形的兩條對角線的長?若存在,求出這個菱形的面積;若不存在,說明理由.
的菱形的兩條對角線的長?若存在,求出這個菱形的面積;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
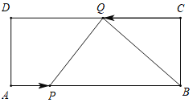
【題目】已知矩形ABCD中,AB=10,BC=4,點P從點A出發,以每秒1個單位長度沿AB方向向B運動,點Q從點C出發,以每秒2個單位長度沿CD方向向D運動,如果P、Q兩點同時出發,問幾秒后以△BPQ是直角三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=90°,且OA,OB分別與反比例函數y=![]() (x>0)、y=﹣
(x>0)、y=﹣![]() (x<0)的圖象交于A,B兩點,則sin∠OAB的值是( )
(x<0)的圖象交于A,B兩點,則sin∠OAB的值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,P為CD邊上一點(DP<CP),∠APB=90°.將△ADP沿AP翻折得到△AD′P,PD′的延長線交邊AB于點M,過點B作BN∥MP交DC于點N.
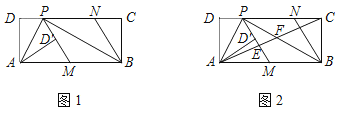
(1)求證:AD2=DPPC;
(2)請判斷四邊形PMBN的形狀,并說明理由;
(3)如圖2,連接AC分別交PM、PB于點E、F.若AD=3DP,探究EF與AE之間的的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,M,N是以AB為直徑的⊙O上的點,且![]() =
=![]() ,弦MN交AB于點C,BM平分∠ABD,MF⊥BD于點F.
,弦MN交AB于點C,BM平分∠ABD,MF⊥BD于點F.
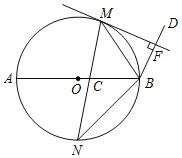
(1)求證:MF是⊙O的切線;
(2)若CN=3,BN=4,求CM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的圖象如圖所示,以下結論:①abc>0;②4ac<b2;③2a+b>0;④其頂點坐標為(
的圖象如圖所示,以下結論:①abc>0;②4ac<b2;③2a+b>0;④其頂點坐標為(![]() ,﹣2);⑤當x<
,﹣2);⑤當x<![]() 時,y隨x的增大而減小;⑥a+b+c>0正確的有( )
時,y隨x的增大而減小;⑥a+b+c>0正確的有( )

A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形![]() 的邊長為
的邊長為![]() ,
,![]() 是邊
是邊![]() 上一點,
上一點,![]() ,將
,將![]() ,
,![]() 分別沿折痕
分別沿折痕![]() ,
,![]() 向內折疊,點
向內折疊,點![]() ,
,![]() 在點
在點![]() 處重合,過點
處重合,過點![]() 作
作![]() ,交
,交![]() 的延長線于
的延長線于![]() .則下列結論正確的有( )
.則下列結論正確的有( )
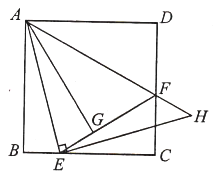
①![]() ;②
;②![]() 為等腰直角三角形;③點
為等腰直角三角形;③點![]() 是
是![]() 的中點;④
的中點;④![]() .
.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與y軸交于點C,與x軸交于A,B兩點,其中點B的坐標為B(4,0),拋物線的對稱軸交x軸于點D,CE∥AB,并與拋物線的對稱軸交于點E現有下列結論:①b2﹣4a<0;②b>0;③5a+b<0;④AD+CE=4.其中正確結論個數為( )
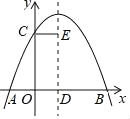
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com