
【題目】我市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧的惠農富農,老張在科技人員的指導下,改良柑橘品種,去年他家的柑橘喜獲豐收,而且質優(yōu)味美,客商聞訊前來采購,經協(xié)商:采購價y(元/噸)與采購量x(噸)之間的函數關系如圖所示.
(1)求y與x之間的函數關系式;
(2)老張種植柑橘的成本是800元/噸,當客商采購量是多少時,老張在這次銷售柑橘時獲利最大?最大利潤是多少?
【答案】
(1)解:當0<x≤10時,y=2000.
當10<x≤20時,設BC滿足的函數關系式為y=kx+b,
∴ ![]() ,解得:
,解得: ![]() ,
,
∴y與x之間的函數關系式為:y=﹣80x+2800
(2)解:當0<x≤10時,老張獲得的利潤為:
w=(2000﹣800)x
=1200x≤12 000,此時老張獲得的最大利潤為12 000元.
當10<x≤20時,老張獲得的利潤為w=(﹣80x+2800﹣800)x
=﹣80(x2﹣25x)=﹣80(x﹣12.5)2+12500.
∴當x=12.5時,利潤w取得最大值,最大值為12500元.
∵12500>12 000,
∴當客商的采購量為12.5噸時,老張在這次買賣中所獲得的利潤最大,最大利潤為12500元
【解析】(1)這是一個分段函數,分別根據當0<x≤10時和當10<x≤20時,求出對應的函數解析式。
(2)先分別求出當0<x≤10時和當10<x≤20時的利潤與x的函數關系式,再分別求出獲利最大時的x的值,再比較大小即可。
【考點精析】通過靈活運用二次函數的最值,掌握如果自變量的取值范圍是全體實數,那么函數在頂點處取得最大值(或最小值),即當x=-b/2a時,y最值=(4ac-b2)/4a即可以解答此題.


 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
【題目】如圖,在一個單位為1的方格紙上,△A1A2A3 , △A3A4A5 , △A5A6A7 , …,是斜邊在x軸上、斜邊長分別為2,4,6,…的等腰直角三角形.若△A1A2A3的頂點坐標分別為A1(2,0),A2(1,﹣1),A3(0,0),則依圖中所示規(guī)律,A2017的橫坐標為( )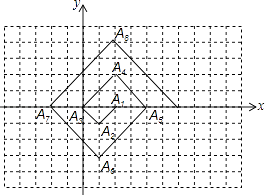
A.1010
B.2
C.1
D.﹣1006
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有實數根,求實數m的取值范圍;
(2)若方程兩實數根分別為x1、x2 , 且滿足x12+x22=10,求實數m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四個全等的直角三角形按圖示方式圍成正方形ABCD,過各較長直角邊的中點作垂線,圍成面積為![]() 的小正方形EFGH,已知AM為Rt△ABM較長直角邊,AM=
的小正方形EFGH,已知AM為Rt△ABM較長直角邊,AM=![]() EF,則正方形ABCD的面積為( )
EF,則正方形ABCD的面積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是△ABC的內心,AE的延長線和△ABC的外接圓相交于點D,連接BD,BE,CE,若∠CBD=32°,則∠BEC的度數為( )
A.128°
B.126°
C.122°
D.120°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E,N,P,G分別在邊AB,BC,CD,DA上,點M,F(xiàn),Q都在對角線BD上,且四邊形MNPQ和AEFG均為正方形,則 ![]() 的值等于 .
的值等于 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從數﹣2,﹣ ![]() ,0,4中任取一個數記為m,再從余下的三個數中,任取一個數記為n,若k=mn,則正比例函數y=kx的圖象經過第三、第一象限的概率是 .
,0,4中任取一個數記為m,再從余下的三個數中,任取一個數記為n,若k=mn,則正比例函數y=kx的圖象經過第三、第一象限的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點P在∠AOB內,點M、N分別是點P關于AO、BO所在直線的對稱點.
(1)若△PEF的周長為20,求MN的長.
(2)若∠O=50°,求∠EPF的度數.
(3)請直接寫出∠EPF與∠O的數量關系是_____________________________

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com