【題目】在平面直角坐標系xOy中，直線y＝2x+m與y軸交于點A，與直線y＝﹣x+4交于點B（3，n），P為直線y＝﹣x+4上一點．
（1）求m，n的值；
（2）在平面直角坐標系系xOy中畫直線y＝2x+m和直線y＝﹣x+4；
（3）當線段AP最短時，求點P的坐標．
【答案】（1）m＝﹣5；（2）詳見解析；（3）
【解析】
（1）首先把點B（3，n）代入直線y=﹣x+4得出n的值，再進一步代入直線y=2x+m求得m的值即可；（2）根據兩點法畫一次函數圖形即可；（3）過點A作直y=﹣x+4的垂線，垂足為P，進一步利用等腰直角三角形的性質和（1）中與y軸交點的坐標特征解決問題．
解：（1）∵點B（3，n）在直線上y＝﹣x+4，
∴n＝1，B（3，1）
∵點B（3，1）在直線上y＝2x+m上，
∴m＝﹣5．
（2）在坐標系中畫出y＝2x﹣5，y＝﹣x+4，如圖①，
（3）過點A作直線y＝﹣x+4的垂線，垂足為P，如圖②
，
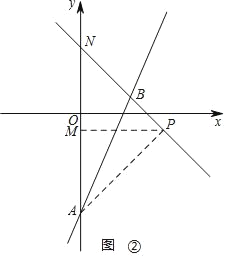此時線段AP最短．
∴∠APN＝90°，
∵直線y＝﹣x+4與y軸交點N（0，4），直線y＝2x﹣5與y軸交點A（0，﹣5），
∴AN＝9，∠ANP＝45°，
∴AM＝PM＝
，
∴OM＝
∴．
陽光考場單元測試卷系列答案
名校聯盟沖刺卷系列答案
名校提分一卷通系列答案科目：初中數學 來源： 題型：
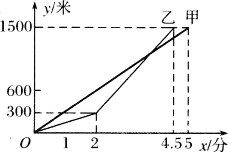
【題目】甲、乙兩人進行1500米比賽，在比賽時，兩人所跑的路程y(米)與所用的時間x(分)間的函數關系如圖所示，解答下列問題：
(1)求甲的速度等于多少米/分；
(2)當乙到終點時，甲距離終點有多遠；
(3)乙在距終點多遠處追上了甲.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在矩形ABCD中，∠ADC的平分線DE與BC邊所在的直線交于點E，點P是線段DE上一定點（其中EP<PD）
（1）如圖1，若點F在CD邊上（不與D重合），將∠DPF繞點P逆時針旋轉90°后，角的兩邊PD、PF分別交射線DA于點H、G．
①求證：PG=PF；
②探究：DF、DG、DP之間有怎樣的數量關系，并證明你的結論．
（2）拓展：如圖2，若點F在CD的延長線上（不與D重合），過點P作PG⊥PF，交射線DA于點G，你認為（1）中DE、DG、DP之間的數量關系是否仍然成立？若成立，給出證明；若不成立，請寫出它們所滿足的數量關系式，并說明理由．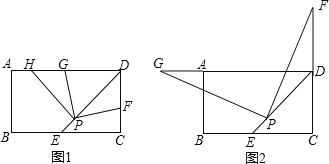
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（2011貴州安順，17，4分）已知：如圖，O為坐標原點，四邊形OABC為矩形，A(10，0)，C(0，4)，點D是OA的中點，點P在BC上運動，當△ODP是腰長為5的等腰三角形時，則P點的坐標為 ．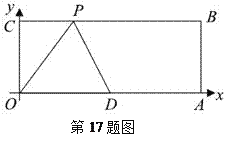
查看答案和解析>>
科目：初中數學 來源： 題型：
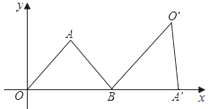
【題目】如圖，△AOB為等腰三角形，頂點A的坐標（2，
），底邊OB在x軸上．將△AOB繞點B按順時針方向旋轉一定角度后得△A′O′B，點A的對應點A′在x軸上，則點O′的坐標為（ ）
A. （
，
） B. （
，
） C. （，） D. （，4
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為預防傳染病，某校定期對教室進行“藥熏消毒”．已知藥物燃燒階段，室內每立方米空氣中的含藥量 
與藥物在空氣中的持續時間
成正比例；燃燒后，
與
成反比例（如圖所示）．現測得藥物
分鐘燃完，此時教室內每立方米空氣含藥量為
．根據以上信息解答下列問題：
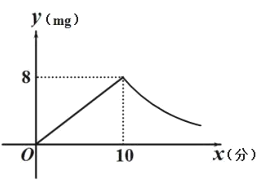
（1）分別求出藥物燃燒時及燃燒后 關于
的函數表達式．
（2）當每立方米空氣中的含藥量低于
時，對人體方能無毒害作用，那么從消毒開始，在哪個時段消毒人員不能停留在教室里？
（3）當室內空氣中的含藥量每立方米不低于
的持續時間超過
分鐘，才能有效殺滅某種傳染病毒．試判斷此次消毒是否有效，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2019年10月27日，軍運會閉幕，軍運村對武漢市民正式銷售，此樓盤開盤均價20000元/ m2，為了加快資金回籠，房地產開發商決定將價格下調10%對外銷售，并在此基礎上再給予以下三種優惠方案供客戶選擇：
①一次性付款可以再打9.8折銷售；
②一次性付款，不享受折上折，但可送兩年物業管理費（物業管理費是每平方米每月3元），再一次性送30000元裝修費；
③如果先付總房款的一半，可送一年的物業管理費，再一次性送10000元裝修費，但是一年后必須一次性付清余下的房款．（注：該年將錢存入銀行，銀行的年利率為3%）
(1)若所購房屋面積為a m2，分別用含a的代數式表示這三種方案的買房費用。
(2)某客戶準備購買其中一套100 m2的房子，如果該客戶有能力一次性付清所有房費，請問他該選擇哪種付款方案更優惠？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，A（-5，0），B（-3，0），點C在y軸的正半軸上，∠CBO=45°，CD∥AB．∠CDA=90°．點P從點Q（4，0）出發，沿x軸向左以每秒1個單位長度的速度運動，運動時時間t秒．
（1）求點C的坐標；
（2）當∠BCP=15°時，求t的值；
（3）以點P為圓心，PC為半徑的⊙P隨點P的運動而變化，當⊙P與四邊形ABCD的邊（或邊所在的直線）相切時，求t的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
