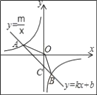
【題目】已知A（﹣4，2）、B（n，﹣4）是一次函數y=kx+b的圖象與反比例函數y=
的圖象的兩個交點；
（1）求此反比例函數和一次函數的解析式；
（2）根據圖象寫出使一次函數的值小于反比例函數的值的x的取值范圍；
（3）求△AOB的面積．
【答案】（1）y=﹣x﹣2；（2）﹣4＜x＜0或x＞2時；（3）設6．
【解析】試題分析：（1）根據點A的坐標求出反比例函數解析式，根據反比例函數解析式，求出點B的橫坐標n，再根據點A、B求出一次函數解析式；
（2）通過觀察圖象，直接得到結果．
（3）設一次函數與y軸交點是C，可把△AOB分成兩個三角形△AOC、△BOC，分別求出它們的面積．
試題解析：（1）由于點A在反比例函數y=
的圖象上，
所以2=
，所以m=﹣8，
即反比例函數解析式為y=
；
∵點B在反比例函數圖象上，所以n×（﹣4）=﹣8，
∴n=2．
因為點A、B在一次函數y=kx+b的圖象上，
∴
∴k=﹣1，b=﹣2，
∴一次函數解析式為：y=﹣x﹣2．
（2）由圖象知，當﹣4＜x＜0或x＞2時，一次函數的值小于反比例函數的值．
（3）設一次函數圖象與y軸交于點C，點A、B的橫坐標分別用xA，xB表示．
則C（0，﹣2），所以OC=2，
∵S△AOB=S△OBC+S△AOC
=
OC×|xB|+
OC×|xA|
=
×2×2+
×2×4
=6．
答：△AOB的面積是6．
期末沖刺100分創新金卷完全試卷系列答案科目：初中數學 來源： 題型：
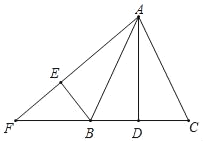
【題目】如圖，△ABC中，AB＝AC，D是BC邊的中點，點E與點D關于AB對稱，連接AE、BE，分別延長AE、CB交于點F，若∠F＝48°，則∠C的度數是（ ）
A. 21°B. 52°C. 69°D. 74°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在
中，
，將繞點
順時針旋轉
至
，點
的對應點分別是
，連接
線段
與線段
交于點M，連接
．
（1）如圖1，求證：
；
（2）如圖1，求證：OM平分
；
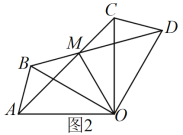
（3）如圖2，若
，求
的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖（1），在△ABC中，∠A=62°，∠ABD=20°，∠ACD=35°，求∠BDC的度數．
（2）圖（1）所示的圖形中，有點像我們常見的學習用品--圓規．我們不妨把這樣圖形叫做“規形圖”，觀察“規形圖”圖（2），試探究∠BDC與∠A、∠B、∠C之間的數量關系，并說明理由．
（3）請你直接利用以上結論，解決以下問題：
①如圖（3），把一塊三角尺XYZ放置在△ABC上，使三角尺的兩條直角邊XY、XZ恰好經過點B、C，若∠A=42°，則∠ABX+∠ACX= °．
②如圖（4），DC平分∠ADB，EC平分∠AEB，若∠DAE=60°，∠DBE=140°，求∠DCE的度數．
③如圖（5），∠ABD，∠ACD的10等分線相交于點G1、G2…、G9，若∠BDC=140°，∠BG1C=68°，求∠A的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
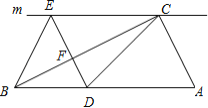
【題目】如圖，在
中，
，過點
的直線
，
為
邊上一點，過點作
交直線
于點
，垂足為點
，連結
、
．
（1）求證：
；
（2）當點是中點時，四邊形
是什么特殊四邊形？說明你的理由；
（3）若點是中點，當四邊形是正方形時，則
大小滿足什么條件？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，矩形ABCD中，AB＝
，AD＝4，在BC邊上取點E，使BE＝AB，將△ABE向左平移到△DCF的位置，得到四邊形AEFD．
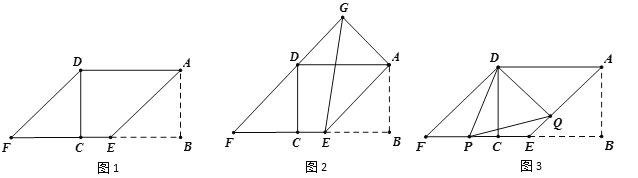
（1）求證：四邊形AEFD是菱形；
（2）如圖2，將△DCF繞點D旋轉至△DGA，連接GE，求線段GE的長；
（3）如圖3，設P、Q分別是EF、AE上的兩點，且∠PDQ=67.5°，試探究線段PF、AQ、PQ之間的數量關系，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商店購進一種商品，每件商品進價30元．試銷中發現這種商品每天的銷售量y（件）與每件銷售價x（元）的關系數據如下：
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
（1）已知y與x滿足一次函數關系，根據上表，求出y與x之間的關系式.（不寫出自變量x的取值范圍）；
（2）如果商店銷售這種商品，每天要獲得150元，那么每件商品的銷售價應定為多少元？
（3）設該商店每天銷售這種商品所獲利潤為w（元），求出w與x之間的關系式，并求出每件商品銷售價定為多少元時利潤最大？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD為矩形，點E是邊BC的中點，AF∥ED，AE∥DF
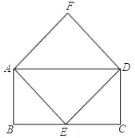
（1）求證：四邊形AEDF為菱形；
（2）試探究：當AB：BC＝ ，菱形AEDF為正方形？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P是矩形ABCD的對角線AC上一點，過點P作EF∥BC，分別交AB，CD于點E，F，連接PB，PD.若AE＝2，PF＝8.則圖中陰影部分的面積為___．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com