
已知拋物線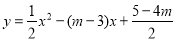 .
.
(1)求證:無論 為任何實數,拋物線與
為任何實數,拋物線與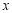 軸總有兩個交點;
軸總有兩個交點;
(2)若A 、B
、B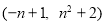 是拋物線上的兩個不同點,求拋物線的表達式和
是拋物線上的兩個不同點,求拋物線的表達式和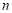 的值;
的值;
(3)若反比例函數 的圖象與(2)中的拋物線在第一象限內的交點的橫坐標為
的圖象與(2)中的拋物線在第一象限內的交點的橫坐標為 ,且滿足2<
,且滿足2< <3,求k的取值范圍.
<3,求k的取值范圍.
(2)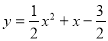 ,
, (3)5<k<18
(3)5<k<18
【解析】
試題分析:(1)根據拋物線的圖像與性質可知其與x軸交點的判定條件是 ,因此可由判別式得證結果;
,因此可由判別式得證結果;
(2)根據題意可求得拋物線的對稱軸,且有A,B的點可判斷它們是對稱點,根據對稱性可求出m的值,求得拋物線的解析式,然后把A點的坐標代入解析式可求得n的值;
(3)根據二次函數的增減性以及反比例函數的圖像與性質,可以判斷出兩函數之間的大小關系,構成不等式,從而解出k的取值范圍.
試題解析:(1)證明:令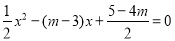 .
.
得

 .
.
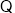 不論m為任何實數,都有(m-1)2+3>0,即△>0.
不論m為任何實數,都有(m-1)2+3>0,即△>0.
∴不論m為任何實數,拋物線與x軸總有兩個交點.
 (2)【解析】
(2)【解析】
拋物線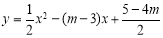 的對稱軸為
的對稱軸為
∵拋物線上兩個不同點A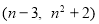 、B
、B 的縱坐標相同,
的縱坐標相同,
∴點A和點B關于拋物線的對稱軸對稱,則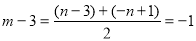 .
.
∴ .
.
∴拋物線的解析式為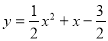 .
.
∵A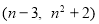 在拋物線
在拋物線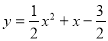 上,
上,
∴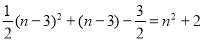 .
.
化簡,得 .
.
∴  .
.
(3)當2< <3時,對于
<3時,對于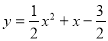 ,y隨著x的增大而增大,
,y隨著x的增大而增大,
對于 ,y隨著x的增大而減小.
,y隨著x的增大而減小.
所以當 時,由反比例函數圖象在二次函數圖象上方,得
時,由反比例函數圖象在二次函數圖象上方,得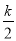 >
> ,
,
解得k>5.
當 時,由二次函數圖象在反比例函數圖象上方,得
時,由二次函數圖象在反比例函數圖象上方,得 >
> ,
,
解得k<18.
所以k的取值范圍為5<k<18.
考點:二次函數的圖像與性質綜合題


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源:2014-2015學年江蘇省太倉市、昆山市七年級上學期期末聯考數學試卷(解析版) 題型:選擇題
已知太陽的半徑約為696000000m,則696000000這個數用科學記數法可表示為 ( ).
A.0.696×109 B.6.96×109
C.6.96×108 D.69.6×107
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河南省三門峽市九年級上學期期末考試數學試卷(解析版) 題型:填空題
如圖,正比例函數 與反比例函數
與反比例函數 相交于點E(
相交于點E(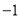 ,2),若
,2),若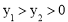 ,則
,則 的取值范圍為 .
的取值范圍為 .

查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市房山區九年級上學期期末考試數學試卷(解析版) 題型:解答題
如圖是一個古代車輪的碎片,小明為求其外圓半徑,連結外圓上的兩點A、B,并使AB與車輪內圓相切于點D,做CD⊥AB交外圓于點C.測得CD=10cm,AB=60cm,求這個車輪的外圓半徑長.

查看答案和解析>>
科目:初中數學 來源:2013-2014學年湖南省祁陽縣九年級下學期期末教學質量檢測數學試卷(解析版) 題型:解答題
甲、乙兩種水稻試驗品種連續5年的平均單位面積產量如下(單位:噸/公頃):
品種 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
為使水稻品種的產量比較穩定,根據題中所給的數據,你選擇哪種水稻品種?請說明理由.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省濱海縣七年級上學期期末考試數學試卷(解析版) 題型:選擇題
如果∠1與∠2互補,∠2與∠3互余,則∠1與∠3的關系是
A.∠1=∠3 B.∠1=180°-∠3
C.∠1=90°+∠3 D.∠3=90°+∠1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com