
【題目】如圖,Rt△ABC中,∠BAC=90°,AB=3,AC=6![]() ,點D,E分別是邊BC,AC上的動點,則DA+DE的最小值為_____.
,點D,E分別是邊BC,AC上的動點,則DA+DE的最小值為_____.
【答案】![]()
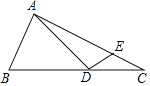
【解析】如圖,作A關于BC的對稱點A',連接AA',交BC于F,過A'作AE⊥AC于E,交BC于D,則AD=A'D,此時AD+DE的值最小,就是A'E的長,根據相似三角形對應邊的比可得結論.
如圖,作A關于BC的對稱點A',連接AA',交BC于F,過A'作AE⊥AC于E,交BC于D,則AD=A'D,此時AD+DE的值最小,就是A'E的長;
Rt△ABC中,∠BAC=90°,AB=3,AC=6![]() ,
,
∴BC=![]() =9,
=9,
S△ABC=![]() ABAC=
ABAC=![]() BCAF,
BCAF,
∴3×6![]() =9AF,
=9AF,
AF=2![]() ,
,
∴AA'=2AF=4![]() ,
,
∵∠A'FD=∠DEC=90°,∠A'DF=∠CDE,
∴∠A'=∠C,
∵∠AEA'=∠BAC=90°,
∴△AEA'∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴A'E=![]() ,
,
即AD+DE的最小值是![]() ,
,
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】探索規律,觀察下面算式,解答問題.
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
…
(1)請猜想:1+3+5+7+9+…+19=________;
(2)請猜想:1+3+5+7+9+…+(2n-1)=________;
(3)試計算:101+103+…+197+199.
查看答案和解析>>
科目:初中數學 來源: 題型:
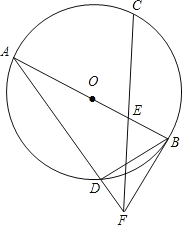
【題目】如圖,AB是⊙O的直徑,![]() ,E是OB的中點,連接CE并延長到點F,使EF=CE.連接AF交⊙O于點D,連接BD,BF.
,E是OB的中點,連接CE并延長到點F,使EF=CE.連接AF交⊙O于點D,連接BD,BF.
(1)求證:直線BF是⊙O的切線;
(2)若OB=2,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
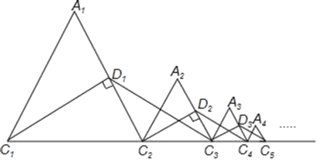
【題目】如圖,等邊△A1C1C2的周長為1,作C1D1⊥A1C2于D1,在C1C2的延長線上取點C3,使D1C3=D1C1,連接D1C3,以C2C3為邊作等邊△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延長線上取點C4,使D2C4=D2C2,連接D2C4,以C3C4為邊作等邊△A3C3C4;…且點A1,A2,A3,…都在直線C1C2同側,如此下去,則△A1C1C2,△A2C2C3,△A3C3C4,…,△AnnCn+1的周長和為_____.(n≥2,且n為整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】ΔABC、ΔCDE都是等邊三角形,AD、BE相交于點O,點M、點N分別是線段AD、BE的中點.
(1)證明: AD=BE.(2)求∠DOE的角度。(3)證明:ΔMNC是等邊三角形.
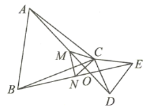
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小江去商店購買簽字筆和筆記本(簽字筆的單價相同,筆記本的單價相同).若購買20支簽字筆和15本筆記本,則他身上的錢會不足25元;若購買19支簽字筆和13本筆記本,則他身上的錢會剩下15元.若小江購買17支簽字筆和9本筆記本,則( )
A.他身上的錢會不足95元 B.他身上的錢會剩下95元
C.他身上的錢會不足105元 D.他身上的錢會剩下105元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com