
【題目】為迎接2022年冬奧會,鼓勵更多的學生參與到志愿服務中來,甲、乙兩所學校組織了志愿服務團隊選拔活動,經過初選,兩所學校各有400名學生進入綜合素質展示環節.為了了解兩所學校這些學生的整體情況,從兩校進人綜合素質展示環節的學生中分別隨機抽取了50名學生的綜合素質展示成績(百分制),并對數據(成績)進行整理、描述和分析.下面給出了部分信息.
a.甲學校學生成績的頻數分布直方圖如下(數據分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
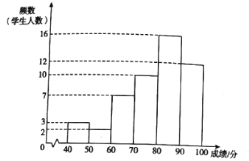
b.甲學校學生成績在![]() 這一組的是:
這一組的是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙學校學生成績的平均數、中位數、眾數、優秀率(85分及以上為優秀)如下:
平均數 | 中位數 | 眾數 | 優秀率 |
83.3 | 84 | 78 | 46% |
根據以上信息,回答下列問題:
(1)甲學校學生A,乙學校學生B的綜合素質展示成績同為83分,這兩人在本校學生中的綜合素質展示排名更靠前的是______(填“A”或“B”);
(2)根據上述信息,推斷_____學校綜合素質展示的水平更高,理由為_____(至少從兩個不同的角度說明推斷的合理性);
(3)若每所學校綜合素質展示的前120名學生將被選入志愿服務團隊,預估甲學校分數至少達到____分的學生才可以入選.
【答案】(1)A;(2)乙;理由見解析;(3)88.5
【解析】
![]() 求得甲校的中位數即可得到結論;
求得甲校的中位數即可得到結論;![]() 根據頻數分布直方圖和表中信息即可得到結論;
根據頻數分布直方圖和表中信息即可得到結論;![]() 求得每所學校被取了50名學生的綜合素質展示的前15名學生將被選入志愿服務團隊,于是得到結論.
求得每所學校被取了50名學生的綜合素質展示的前15名學生將被選入志愿服務團隊,于是得到結論.
解:![]() 甲學校學生成績的中位數為
甲學校學生成績的中位數為![]() ,
,
乙學校學生成績的中位數為84,
故這兩人在本校學生中綜合素質展示排名更靠前的是A,
故答案為A;![]() 根據上述信息,推斷乙學校綜合素質展示的水平更高,理由為:與甲校相比,乙校的中位數更高,說明乙校綜合展示水平較高的同學更多;與甲校相比,乙校的優秀率更高,說明乙校綜合展示水平高分的人數更多;
根據上述信息,推斷乙學校綜合素質展示的水平更高,理由為:與甲校相比,乙校的中位數更高,說明乙校綜合展示水平較高的同學更多;與甲校相比,乙校的優秀率更高,說明乙校綜合展示水平高分的人數更多;
故答案為乙學校,與甲校相比,乙校的中位數更高,說明乙校綜合展示水平較高的同學更多;與甲校相比,乙校的優秀率更高,說明乙校綜合展示水平高分的人數更多![]() ,
,
故甲學校分數至少達到![]() 分的學生才可以入選,
分的學生才可以入選,
故答案為![]() .
.


科目:初中數學 來源: 題型:
【題目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是射線
是射線![]() 上的點,連接
上的點,連接![]() ,將
,將![]() 沿直線
沿直線![]() 翻折得
翻折得![]() .
.
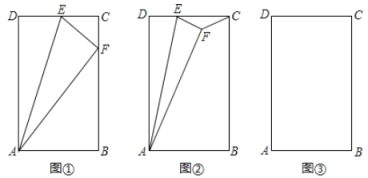
(1)如圖①,點![]() 恰好在
恰好在![]() 上,求證:
上,求證:![]() ∽
∽![]() ;
;
(2)如圖②,點![]() 在矩形
在矩形![]() 內,連接
內,連接![]() ,若
,若![]() ,求
,求![]() 的面積;
的面積;
(3)若以點![]() 、
、![]() 、
、![]() 為頂點的三角形是直角三角形,則
為頂點的三角形是直角三角形,則![]() 的長為 .
的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,弦
的直徑,弦![]() ,
,![]()
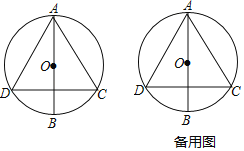
(1)求證:![]() 是等邊三角形.
是等邊三角形.
(2)若點![]() 是
是![]() 的中點,連接
的中點,連接![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() ,若
,若![]() ,求線段
,求線段![]() 的長;
的長;
(3)若![]() 的半徑為4,點
的半徑為4,點![]() 是弦
是弦![]() 的中點,點
的中點,點![]() 是直線
是直線![]() 上的任意一點,將點
上的任意一點,將點![]() 繞點
繞點![]() 逆時針旋轉60°得點
逆時針旋轉60°得點![]() ,求線段
,求線段![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們研究過的圖形中,圓的任何一對平行切線的距離總是相等的,所以圓是“等寬曲線”.除了圓以外,還有一些幾何圖形也是“等寬曲線”,如勒洛三角形(如圖![]() ),它是分別以等邊三角形的每個頂點為圓心,以邊長為半徑,在另兩個頂點間畫一段圓弧,三段圓弧圍成的曲邊三角形. 圖
),它是分別以等邊三角形的每個頂點為圓心,以邊長為半徑,在另兩個頂點間畫一段圓弧,三段圓弧圍成的曲邊三角形. 圖![]() 是等寬的勒洛三角形和圓形滾木的截面圖.
是等寬的勒洛三角形和圓形滾木的截面圖.
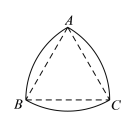

圖![]() 圖
圖![]()
有如下四個結論:
①勒洛三角形是中心對稱圖形
②圖![]() 中,點
中,點![]() 到
到![]() 上任意一點的距離都相等
上任意一點的距離都相等
③圖![]() 中,勒洛三角形的周長與圓的周長相等
中,勒洛三角形的周長與圓的周長相等
④使用截面是勒洛三角形的滾木來搬運東西,會發生上下抖動
上述結論中,所有正確結論的序號是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系![]() 中有點
中有點![]() 和某一函數圖象
和某一函數圖象![]() ,過點
,過點![]() 作
作![]() 軸的垂線,交圖象
軸的垂線,交圖象![]() 于點
于點![]() ,設點
,設點![]() ,
,![]() 的縱坐標分別為
的縱坐標分別為![]() ,
,![]() .如果
.如果![]() ,那么稱點
,那么稱點![]() 為圖象
為圖象![]() 的上位點;如果
的上位點;如果![]() ,那么稱點
,那么稱點![]() 為圖象
為圖象![]() 的圖上點;如果
的圖上點;如果![]() ,那么稱點
,那么稱點![]() 為圖象
為圖象![]() 的下位點.
的下位點.
(1)已知拋物線![]() .
.
① 在點A(-1,0),B(0,-2),C(2,3)中,是拋物線的上位點的是 ;
② 如果點![]() 是直線
是直線![]() 的圖上點,且為拋物線的上位點,求點
的圖上點,且為拋物線的上位點,求點![]() 的橫坐標
的橫坐標![]() 的取值范圍;
的取值范圍;
(2)將直線![]() 在直線
在直線![]() 下方的部分沿直線
下方的部分沿直線![]() 翻折,直線
翻折,直線![]() 的其余部分保持不變,得到一個新的圖象,記作圖象
的其余部分保持不變,得到一個新的圖象,記作圖象![]() .⊙
.⊙![]() 的圓心
的圓心![]() 在
在![]() 軸上,半徑為
軸上,半徑為![]() .如果在圖象
.如果在圖象![]() 和⊙
和⊙![]() 上分別存在點
上分別存在點![]() 和點F,使得線段EF上同時存在圖象
和點F,使得線段EF上同時存在圖象![]() 的上位點,圖上點和下位點,求圓心
的上位點,圖上點和下位點,求圓心![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知C為線段AB中點,∠ACM=α.Q為線段BC上一動點(不與點B重合),點P在射線CM上,連接PA,PQ,記BQ=kCP.
(1)若α=60°,k=1,
①如圖1,當Q為BC中點時,求∠PAC的度數;
②直接寫出PA、PQ的數量關系;
(2)如圖2,當α=45°時.探究是否存在常數k,使得②中的結論仍成立?若存在,寫出k的值并證明;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 在線段
在線段![]() 上,以
上,以![]() 為直徑的
為直徑的![]() 與
與![]() 相交于點
相交于點![]() ,與
,與![]() 相交于點
相交于點![]() ,
,![]() .
.
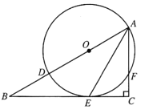
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)在(1)的條件下,判斷以![]() 為頂點的四邊形為哪種特殊四邊形,并說明理由.
為頂點的四邊形為哪種特殊四邊形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于
的圖象交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點.
兩點.

(1)求一次函數的解析式;
(2)根據圖象直接寫出![]() ,時
,時![]() 的取值范圍;
的取值范圍;
(3)求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在以“放飛青春夢想,展示你我風采”為主題的校園文化藝術節期間,舉辦了![]() .歌唱,
.歌唱,![]() .舞蹈,
.舞蹈,![]() .繪畫,
.繪畫,![]() .演講共四個類別的比賽,要求每位學生必須參加且僅能參加一個類別.小紅隨機調查了部分學生的報名情況,并繪制了下列兩幅不完整的統計圖,請根據統計圖中的信息解答下列問題:
.演講共四個類別的比賽,要求每位學生必須參加且僅能參加一個類別.小紅隨機調查了部分學生的報名情況,并繪制了下列兩幅不完整的統計圖,請根據統計圖中的信息解答下列問題:
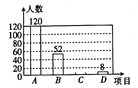
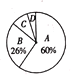
(1)本次調查的學生總人數是多少?扇形統計圖中“![]() ”部分的圓心角度數是多少?
”部分的圓心角度數是多少?
(2)請將條形統計圖補充完整.
(3)若全校共有1500名學生,請估計該校報名參加繪畫和演講兩個類別的比賽的學生共有多少人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com