
【題目】為增強學生的身體素質,教育行政部門規定每位學生每天參加戶外活動的平均時間不少于1小時. 為了解學生參加戶外活動的情況,對部分學生參加戶外活動的時間進行抽樣調查,并將調查結果繪制作成如下兩幅不完整的統計圖,

請你根據圖中提供的信息解答下列問題:
(1)在這次調查中共調查了多少名學生?
(2)求戶外活動時間為1.5小時的人數,并補充頻數分布直方圖;
(3)戶外活動時間的眾數和中位數分別是多少?
(4)若該市共有20000名學生,大約有多少學生戶外活動的平均時間符合要求?
【答案】(1)50;(2)12;(3)中數是1小時,中位數是1小時;(4)16000人.
【解析】試題分析:(1)根據戶外活動時間是0.5小時的有10人,所占的百分比是20%,據此即可求得調查的總人數;
(2)用總人數乘以對應的百分比即可求得人數,從而補全直方圖;
(3)根據眾數、中位數的定義即可求解;
(4)利用總人數乘以對應的比分比即可求解.
試題解析:(1)調查的總人數是10÷20%=50(人);
(2)戶外活動時間是1.5小時的人數是50×24%=12(人),
 ;
;
(3)中數是1小時,中位數是1小時;
(4)學生戶外活動的平均時間符合要求的人數是20000×(1-20%)=16000(人).
答:大約有16000學生戶外活動的平均時間符合要求.


科目:初中數學 來源: 題型:
【題目】【探索新知】
如圖1,射線OC在∠AOB的內部,圖中共有3個角:∠AOB、∠AOC和∠BOC,若其中有一個角的度數是另一個角度數的兩倍,則稱射線OC是∠AOB的“妙分線”.
【解決問題】
(1)如圖2,若∠MPN= ![]() ,且射線PQ是∠MPN的“妙分線”,則∠NPQ= ____ .(用含
,且射線PQ是∠MPN的“妙分線”,則∠NPQ= ____ .(用含![]() 的代數式表示出所有可能的結果)
的代數式表示出所有可能的結果)
【深入研究】
如圖2,若∠MPN=54°,且射線PQ繞點P從PN位置開始,以每秒8°的速度順時針旋轉,當PQ與PN成![]() 時停止旋轉,旋轉的時間為t秒.
時停止旋轉,旋轉的時間為t秒.
(2)當t為何值時,射線PM是∠QPN的“妙分線”.
(3)若射線PM同時繞點P以每秒6°的速度順時針旋轉,并與PQ同時停止.請求出當射線PQ 是∠MPN的“妙分線”時t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A樣本的數據如下:72,73,76,76,77,78,78,78,B樣本的數據恰好是A樣本數據每個都加2,則A,B兩個樣本的下列統計量對應相同的是( )
A.平均數
B.標準差
C.中位數
D.眾數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在四邊形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°. 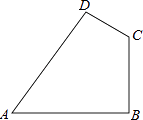
(1)猜想的∠A與∠C關系;
(2)求出四邊形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,已知線段AB=20cm,CD=2cm,線段CD在線段AB上運動,E、F分別是AC、BD的中點.
(1)若AC=4cm,則EF=_________cm.
(2)當線段CD在線段AB上運動時,試判斷EF的長度是否發生變化?如果不變請求出EF的長度,如果變化,請說明理由.
(3)我們發現角的很多規律和線段一樣,如圖②已知![]() 在
在![]() 內部轉動,OE、OF分別平分
內部轉動,OE、OF分別平分![]() 在
在![]() ,則
,則![]() 、
、![]() 和
和![]() 有何關系,請直接寫出_______________________.
有何關系,請直接寫出_______________________.
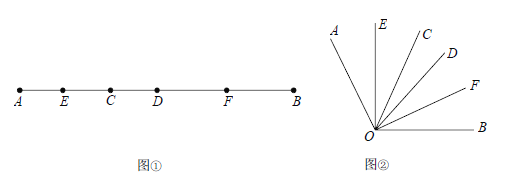
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】判斷正誤,并說明理由
(1)給定一組數據,那么這組數據的眾數有可能不唯一;理由
(2)給定一組數據,那么這組數據的平均數一定是這組數據中的一個數;
理由
(3)n個數的中位數一定是這n個數中的某一個;理由
(4)求9個數據(x1、x2、……、x9 , 其平均數為m)的標準差S, 計算公式為: ![]() ;理由
;理由
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com