【題目】如圖，在平面直角坐標系中，將線段AB繞點A按逆時針方向旋轉90°后，得到線段AB′，則點B′的坐標為__________．
【答案】（4,2）
【解析】
試題考查知識點：圖形繞固定點旋轉
思路利用網格做直角三角形AMB，讓△AMB逆時針旋轉90°，也就使AB逆時針旋轉了90°，由
輕易得知
，圖中的AB′就是旋轉后的位置。點B′剛好在網格格點上，坐標值也就非常明顯了。
具體解答過程：
如圖所示。做AM∥x軸、BM∥y軸，且AM與BM交于M點，則△AMB為直角三角形,
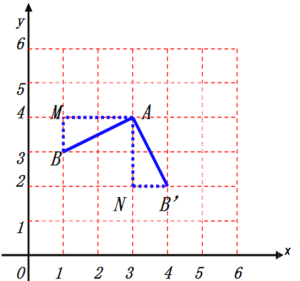
線段AB繞點A按逆時針方向旋轉90°，可以視為將△AMB逆時針方向旋轉90°（）得到△ANB′后的結果。
∴,AN⊥x軸，NB′⊥y軸，點B′剛好落在網格格點處
∵線段AB上B點坐標為（1，3）
∴點B′的橫坐標值為：1+3=4；縱坐標值為：3-1=2
即點B′的坐標為（4,2）
閱讀快車系列答案科目：初中數學 來源： 題型：
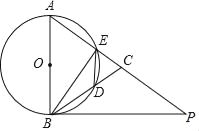
【題目】在△ABC中，AB＝AC，以AB為直徑的⊙O交AC于點E，交BC于點D，P為AC延長線上一點，且∠PBC＝
∠BAC，連接DE，BE．
（1）求證：BP是⊙O的切線；
（2）若sin∠PBC＝
，AB＝10，求BP的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠C＝90°．點O是AB的中點，邊AC＝6，將邊長足夠大的三角板的直角頂點放在點O處，將三角板繞點0旋轉，始終保持三角板的直角邊與AC相交，交點為點E，另條直角邊與BC相交，交點為D，則等腰直角三角板的直角邊被三角板覆蓋部分的兩條線段CD與CE的長度之和為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知∠BAC＝65°，D為∠BAC內部一點，過D作DB⊥AB于B，DC⊥AC于C，設點E、點F分別為AB、AC上的動點，當△DEF的周長最小時，∠EDF的度數為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖所示，在△ABC中，∠B=90°，AB=5cm，BC=7cm，點P從點A開始沿AB邊向點B以1cm/s的速度移動，點Q從點B開始沿BC邊向點C以2cm/s的速度移動.
（1）如果P，Q分別從A，B同時出發，那么幾秒后，△PBQ的面積等于4cm2？
（2）如果P，Q分別從A，B同時出發，那么幾秒后，△PBQ中PQ的長度等于5cm？
（3）在（1）中，當P，Q出發幾秒時，△PBQ有最大面積?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在“基善一日捐冊”活動中，為了解某校學生的捐款情況，抽樣調查了該校部分學生的捐款數（單位:元），并繪制成下面的統計圖．
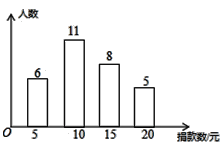
（1）本次調查中，一共調查了________名同學；
（2）抽查學生捐款數額的眾數是_______元，中位數是_______元；
（3）該校共有600名學生參與捐款，請你估計該校學生捐款不少于15元的人數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（閱讀理解）
截長補短法，是初中數學兒何題中一種輸助線的添加方法，截長就是在長邊上載取一條線段與某一短邊相等，補短是通過在一條短邊上延長一條線段與另一短邊相等，從而解決問題.
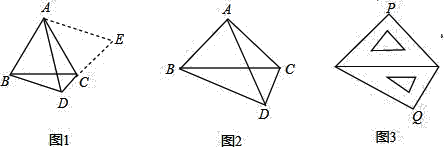
（1）如圖1，△ABC是等邊三角形，點D是邊BC下方一點，∠BDC＝120°，探索線段DA、DB、DC之間的數量關系.
解題思路：延長DC到點E，使CE＝BD.連接AE，根據∠BAC＋∠BDC＝180°，可證∠ABD＝∠ACE,易證得△ABD≌△ACE，得出△ADE是等邊三角形，所以AD＝DE，從而探尋線段DA、DB、DC之間的數量關系.
根據上述解題思路，請直接寫出DA、DB、DC之間的數量關系是___________
（拓展延伸）
（2）如圖2，在Rt△ABC中，∠BAC＝90°，AB＝AC.若點D是邊BC下方一點，∠BDC＝90°，探索線段DA、DB、DC之間的數量關系，并說明理由;
（知識應用）
（3）如圖3,一副三角尺斜邊長都為14cm，把斜邊重疊擺放在一起，則兩塊三角尺的直角項點之間的距離PQ的長為________cm.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，有一塊含30°角的直角三角板OAB的直角邊BO的長恰與另一塊等腰直角三角板ODC的斜邊OC的長相等，把這兩塊三角板放置在平面直角坐標系中，且OB＝3
.
(1)若某反比例函數的圖象的一個分支恰好經過點A，求這個反比例函數的解析式；
(2)若把含30°角的直角三角板繞點O按順時針方向旋轉后，斜邊OA恰好落在x軸上，點A落在點A′處，試求圖中陰影部分的面積．(結果保留π)
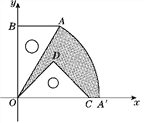
【答案】(1)反比例函數的解析式為y＝
；(2)S陰影＝6π－
.
【解析】分析：（1）根據tan30°=
，求出AB，進而求出OA，得出A的坐標，設過A的雙曲線的解析式是y=
，把A的坐標代入求出即可；（2）求出∠AOA′，根據扇形的面積公式求出扇形AOA′的面積，求出OD、DC長，求出△ODC的面積，相減即可求出答案．
本題解析：
(1)在Rt△OBA中，∠AOB＝30°，OB＝3
，
∴AB＝OB·tan 30°＝3.
∴點A的坐標為(3，3)．
設反比例函數的解析式為y＝
(k≠0)，
∴3＝
，∴k＝9，則這個反比例函數的解析式為y＝
.
(2)在Rt△OBA中，∠AOB＝30°，AB＝3，
sin ∠AOB＝
，即sin 30°＝
，
∴OA＝6.
由題意得：∠AOC＝60°，S扇形AOA′＝
＝6π.
在Rt△OCD中，∠DOC＝45°，OC＝OB＝3，
∴OD＝OC·cos 45°＝3×
＝
.
∴S△ODC＝
OD2＝
＝
.
∴S陰影＝S扇形AOA′－S△ODC＝6π－.
點睛：本題考查了勾股定理、待定系數法求函數解析式、特殊角的三角函數值、扇形的面積及等腰三角形的性質，本題屬于中檔題，難度不大，將不規則的圖形的面積表示成多個規則圖形的面積之和是解答本題的關鍵.
【題型】解答題
【結束】
26
【題目】矩形ABCD一條邊AD＝8，將矩形ABCD折疊，使得點B落在CD邊上的點P處．
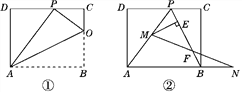
(1)如圖①，已知折痕與邊BC交于點O，連接AP，OP，OA.
① 求證：△OCP∽△PDA；
② 若△OCP與△PDA的面積比為1:4，求邊AB的長．
(2)如圖②，在(1)的條件下，擦去AO和OP，連接BP.動點M在線段AP上(不與點P，A重合)，動點N在線段AB的延長線上，且BN＝PM，連接MN交PB于點F，作ME⊥BP于點E.試問動點M，N在移動的過程中，線段EF的長度是否發生變化？若不變，求出線段EF的長度；若變化，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知四邊形ABCD∽四邊形A′B′C′D′，且AB∶BC∶CD∶DA＝20∶15∶9∶8，四邊形A′B′C′D′的周長為26，求四邊形A′B′C′D′各邊的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com