
【題目】(操作發現)
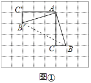
如圖①,在邊長為1個單位長度的小正方形組成的網格中,△ABC的三個頂點均在格點上.

(1)請按要求畫圖:將△ABC繞點A按順時針方向旋轉90°,點B的對應點為B′,點C的對應點為C′,連接BB′;
(2)在(1)所畫圖形中,∠AB′B=____.
(問題解決)
(3)如圖②,在等邊三角形ABC中,AC=7,點P在△ABC內,且∠APC=90°,∠BPC=120°,求△APC的面積.
小明同學通過觀察、分析、思考,對上述問題形成了如下想法:
想法一:將△APC繞點A按順時針方向旋轉60°,得到△AP′B,連接PP′,尋找PA,PB,PC三條線段之間的數量關系;
想法二:將△APB繞點A按逆時針方向旋轉60°,得到△AP′C′,連接PP′,尋找PA,PB,PC三條線段之間的數量關系.…
請參考小明同學的想法,完成該問題的解答過程.(一種方法即可)
【答案】(1)如圖,△AB′C′即為所求;見解析;(2)45°;(3)S△APC=![]() .
.
【解析】
(1)如圖所示,△AB′C′即為所求;
(2)利用等腰三角形的性質即可解決問題;
【問題解決】
結論:PA2+PB2=PC2.
證法一:將△APC繞點A按順時針方向旋轉60°,得到△AP′B,連接PP′,尋找PA,PB,PC三條線段之間的數量關系;
證法二:將△APB繞點A按逆時針方向旋轉60°,得到△AP′C′,連接PP′,尋找PA,PB,PC三條線段之間的數量關系.
(1)如圖,△AB′C′即為所求;
(2)∵△ABB′是等腰直角三角形,
∴∠AB′B=45°.
故答案為45°;
(3)如圖②,

∵將△APB繞點A按逆時針方向旋轉60°,得到△AP′C′,
∴△APP′是等邊三角形,∠AP′C=∠APB=360°﹣90°﹣120°=150°,
∴PP′=AP,∠AP′P=∠APP′=60°,∴∠PP′C=90°,∠P′PC=30°,
∴PP′= ![]() PC,即AP=
PC,即AP= ![]() PC
PC
∵∠APC=90°,∴AP2+PC2=AC2 , 即(![]() PC)2+PC2=72 , ∴PC=
PC)2+PC2=72 , ∴PC=![]() ,
,
∴AP=![]() ,∴S△APC=
,∴S△APC=![]() APPC=
APPC=![]()


科目:初中數學 來源: 題型:
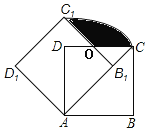
【題目】如圖,邊長為1的正方形ABCD繞點A逆時針旋轉45°后得到正方形AB1C1D1,邊B1C1與CD交于點O,則圖中陰影部分的面積是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
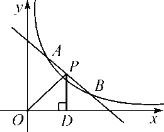
【題目】如圖,一次函數y=-x+b與反比例函數y=![]() (x>0)的圖象交于點A(m,3)和B(3,1).
(x>0)的圖象交于點A(m,3)和B(3,1).
(1)求一次函數和反比例函數的解析式;
(2)點P(x,y)是直線AB上在第一象限內的一個點,過點P作PD⊥x軸于點D,連接OP,令△POD的面積為S,當S>![]() 時,直接寫出點P橫坐標x的取值范圍.
時,直接寫出點P橫坐標x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
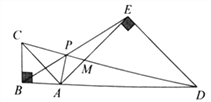
【題目】如圖,點![]() 在線段
在線段![]() 上,在
上,在![]() 的同側作等腰
的同側作等腰![]() 和等腰
和等腰![]() ,
,![]() 與
與![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() .對于下列結論:
.對于下列結論:
①![]() ;②
;②![]() ;③
;③![]() .其中正確的是( )
.其中正確的是( )
A. ①②③ B. ① C. ①② D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知函數![]() (x>0)的圖象經過點A,B,點A的坐標為(1,2).過點A作AC∥y軸,AC=1(點C位于點A的下方),過點C作CD∥x軸,與函數的圖象交于點D,過點B作BE⊥CD,垂足E在線段CD上,連接OC,OD.
(x>0)的圖象經過點A,B,點A的坐標為(1,2).過點A作AC∥y軸,AC=1(點C位于點A的下方),過點C作CD∥x軸,與函數的圖象交于點D,過點B作BE⊥CD,垂足E在線段CD上,連接OC,OD.
(1)求△OCD的面積;
(2)當BE=![]() AC時,求CE的長.
AC時,求CE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
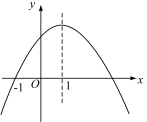
【題目】如圖是二次函數y=ax2+bx+c的圖象,其對稱軸為x=1,下列結論:①abc>0;②2a+b=0;③4a+2b+c<0;④若(-![]() ,y1),(
,y1),(![]() ,y2)是拋物線上兩點,則y1<y2, 其中結論正確的是________.
,y2)是拋物線上兩點,則y1<y2, 其中結論正確的是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com