
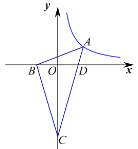
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() ,點
,點![]() 在反比例函數
在反比例函數![]() 的圖象上,且
的圖象上,且![]() 軸平分
軸平分![]() ,求
,求![]() _____.
_____.
【答案】![]()
【解析】
要求k的值,通常可求A的坐標,可作x軸的垂線,構造相似三角形,利用CD=4AD和C(0,-4)可以求出A的縱坐標,再利用三角形相似,設未知數,由相似三角形對應邊成比例,列出方程,求出待定未知數,從而確定點A的坐標,進而確定k的值.
解:過A作AE⊥x軸,垂足為E,
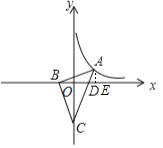
∵C(0,-4),
∴OC=4,
∵∠AED=∠COD=90°,∠ADE=∠CDO
∴△ADE∽△CDO,
![]() ,
,
∴AE=1;
又∵y軸平分∠ACB,CO⊥BD,
∴BO=OD,
∵∠ABC=90°,
∴∠OCD=∠DAE=∠ABE=∠BCE,
∵∠DOC=∠ADE=90°
∴△ABE~△COD,
∴![]()
設DE=n,則BO=OD=4n,BE=9n,
∴![]() ,
,
∴![]() ,
,
∴OE=5n=![]() ,
,
故點A(![]() ,1),
,1),
∴k=![]() ×1=
×1=![]()
故答案為:![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
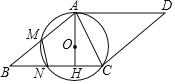
【題目】已知:如圖△ABC內接于⊙O,OH⊥AC于H,過A點的切線與OC的延長線交于點D,∠B=30°,OH=5![]() .請求出:
.請求出:

(1)∠AOC的度數;
(2)△OAC的面積;
(3)線段AD的長(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將![]() 放在每個小正方形的邊長為1的網格中,點A,點B,點C均落在格點上.
放在每個小正方形的邊長為1的網格中,點A,點B,點C均落在格點上.
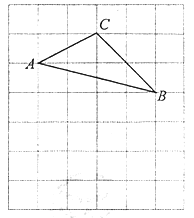
(I)計算![]() 的值等于____________;
的值等于____________;
(Ⅱ)請在如圖所示的網格中,用無刻度的直尺,畫出一個以AB為一邊、面積等于![]() 的矩形,并簡要說明畫圖方法(不要求證明)_____________.
的矩形,并簡要說明畫圖方法(不要求證明)_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角三角形的直角頂點在坐標原點,∠OAB=30°,若點A在反比例函數y=![]() (x>0)的圖象上,則經過點B的反比例函數解析式為( )
(x>0)的圖象上,則經過點B的反比例函數解析式為( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
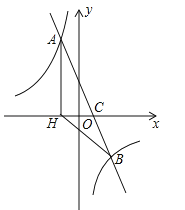
【題目】如圖,在平面直角坐標系中,一次函數y=ax+b(a≠0)的圖象與反比例函數![]() (k≠0)的圖象交于A、B兩點,與x軸交于點C,過點A作AH⊥x軸于點H,點O是線段CH的中點,AC=
(k≠0)的圖象交于A、B兩點,與x軸交于點C,過點A作AH⊥x軸于點H,點O是線段CH的中點,AC=![]() ,cos∠ACH=
,cos∠ACH=![]() ,點B的坐標為(4,n)
,點B的坐標為(4,n)
(1)求該反比例函數和一次函數的解析式;
(2)求△BCH的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】超市有![]() ,
,![]() 兩種型號的瓶子,其容量和價格如表,小張買瓶子用來分裝15升油(瓶子都裝滿,且無剩油);當日促銷活動:購買
兩種型號的瓶子,其容量和價格如表,小張買瓶子用來分裝15升油(瓶子都裝滿,且無剩油);當日促銷活動:購買![]() 型瓶3個或以上,一次性返還現金5元,設購買
型瓶3個或以上,一次性返還現金5元,設購買![]() 型瓶
型瓶![]() (個),所需總費用為
(個),所需總費用為![]() (元),則下列說法不一定成立的是( )
(元),則下列說法不一定成立的是( )
型號 | A | B |
單個盒子容量(升) | 2 | 3 |
單價(元) | 5 | 6 |
A.購買![]() 型瓶的個數是
型瓶的個數是![]() 為正整數時的值B.購買
為正整數時的值B.購買![]() 型瓶最多為6個
型瓶最多為6個
C.![]() 與
與![]() 之間的函數關系式為
之間的函數關系式為![]() D.小張買瓶子的最少費用是28元
D.小張買瓶子的最少費用是28元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在菱形![]() 中,
中,![]() ,
,![]() .動點
.動點![]() 從點
從點![]() 出發,沿
出發,沿![]() 邊以每秒1個單位長度的速度運動到點
邊以每秒1個單位長度的速度運動到點![]() 時停止,連接
時停止,連接![]() ,點
,點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱,連接
對稱,連接![]() ,
,![]() ,設運動時間為
,設運動時間為![]() (秒).
(秒).

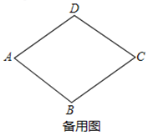
(1)菱形![]() 對角線
對角線![]() 的長為 ;
的長為 ;
(2)當點![]() 恰在
恰在![]() 上時,求t的值;
上時,求t的值;
(3)當![]() 時,求
時,求![]() 的周長;
的周長;
(4)直接寫出在整個運動過程中,點![]() 運動的路徑長.
運動的路徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店銷售甲、乙兩種圓規,當銷售5只甲種、1只乙種圓規,可獲利潤25元,銷售6只甲種、3只乙種圓規,可獲利潤39元.
(1)問該文具店銷售甲、乙兩種圓規,每只的利潤分別是多少元?
(2)在(1)中,文具店共銷售甲、乙兩種圓規50只,其中甲種圓規為a只,求文具店所獲得利潤P與a的函數關系式,并求當a≥30時P的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 是線段
是線段![]() 上一點,
上一點,![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 的長為半徑作⊙
的長為半徑作⊙![]() ,過點
,過點![]() 作
作![]() 的垂線交⊙
的垂線交⊙![]() 于
于![]() ,
,![]() 兩點,點
兩點,點![]() 在線段
在線段![]() 的延長線上,連接
的延長線上,連接![]() 交⊙
交⊙![]() 于點
于點![]() ,以
,以![]() ,
,![]() 為邊作
為邊作![]() .
.
(1)求證:![]() 是⊙
是⊙![]() 的切線;
的切線;
(2)若![]() ,求四邊形
,求四邊形![]() 與⊙
與⊙![]() 重疊部分的面積;
重疊部分的面積;
(3)若![]() ,
,![]() ,連接
,連接![]() ,求
,求![]() 和
和![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com