
【題目】如圖所示,在△ABC中,![]() ,D、E分別是邊AB、BC上的動點(diǎn),且
,D、E分別是邊AB、BC上的動點(diǎn),且![]() ,連結(jié)AD、AE,點(diǎn)M、N、P分別是CD、AE、AC的中點(diǎn),設(shè)
,連結(jié)AD、AE,點(diǎn)M、N、P分別是CD、AE、AC的中點(diǎn),設(shè)![]() .
.
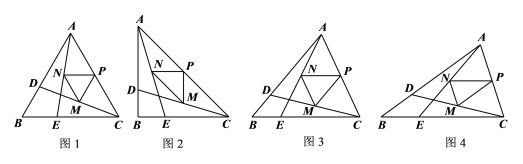
(1)觀察猜想
①在求![]() 的值時,小明運(yùn)用從特殊到一般的方法,先令
的值時,小明運(yùn)用從特殊到一般的方法,先令![]() ,解題思路如下:
,解題思路如下:
如圖1,先由![]() ,得到
,得到![]() ,再由中位線的性質(zhì)得到
,再由中位線的性質(zhì)得到![]() ,
,
![]() ,進(jìn)而得出△PMN為等邊三角形,∴
,進(jìn)而得出△PMN為等邊三角形,∴![]() .
.
②如圖2,當(dāng)![]() ,仿照小明的思路求
,仿照小明的思路求![]() 的值;
的值;
(2)探究證明
如圖3,試猜想![]() 的值是否與
的值是否與![]() 的度數(shù)有關(guān),若有關(guān),請用含
的度數(shù)有關(guān),若有關(guān),請用含![]() 的式子表示出
的式子表示出![]() ,若無關(guān),請說明理由;
,若無關(guān),請說明理由;
(3)拓展應(yīng)用
如圖4,![]() ,點(diǎn)D、E分別是射線AB、CB上的動點(diǎn),且
,點(diǎn)D、E分別是射線AB、CB上的動點(diǎn),且![]() ,點(diǎn)M、N、P分別是線段CD、AE、AC的中點(diǎn),當(dāng)
,點(diǎn)M、N、P分別是線段CD、AE、AC的中點(diǎn),當(dāng)![]() 時,請直接寫出MN的長.
時,請直接寫出MN的長.
【答案】(1)②![]() ;(2)
;(2)![]() 的值與
的值與![]() 的度數(shù)有關(guān),
的度數(shù)有關(guān),![]() ;(3)MN的長為
;(3)MN的長為![]() 或
或![]() .
.
【解析】
(1)②先根據(jù)線段的和差求出![]() ,再根據(jù)中位線定理、平行線的性質(zhì)得出
,再根據(jù)中位線定理、平行線的性質(zhì)得出![]() ,從而可得出
,從而可得出![]() ,然后根據(jù)等腰直角三角形的性質(zhì)即可得;
,然后根據(jù)等腰直角三角形的性質(zhì)即可得;
(2)參照題(1)的方法,得出![]() 為等腰三角形和
為等腰三角形和![]() 的度數(shù),再利用等腰三角形的性質(zhì)即可求出答案;
的度數(shù),再利用等腰三角形的性質(zhì)即可求出答案;
(3)分兩種情況:當(dāng)點(diǎn)D、E分別是邊AB、CB上的動點(diǎn)時和當(dāng)點(diǎn)D、E分別是邊AB、CB的延長線上的動點(diǎn)時,如圖(見解析),先利用等腰三角形的性質(zhì)與判定得出![]() ,再根據(jù)相似三角形的判定與性質(zhì)得出BC、CE的長,由根據(jù)等腰三角形的三線合一性得出
,再根據(jù)相似三角形的判定與性質(zhì)得出BC、CE的長,由根據(jù)等腰三角形的三線合一性得出![]() ,從而可得
,從而可得![]() 的值,最后分別利用(2)的結(jié)論即可得MN的長.
的值,最后分別利用(2)的結(jié)論即可得MN的長.
(1)②![]()
∴![]()
![]()
∴![]() 為等腰直角三角形,
為等腰直角三角形,![]()
∵點(diǎn)M、N、P分別是CD、AE、AC的中點(diǎn)
![]()
![]()
∴![]()
∴![]() 為等腰直角三角形,
為等腰直角三角形,
∴![]()
即![]() ;
;
(2)![]() 的值與
的值與![]() 的度數(shù)有關(guān),求解過程如下:
的度數(shù)有關(guān),求解過程如下:
由(1)可知,![]() ,即
,即![]() 為等腰三角形
為等腰三角形
![]()
如圖5,作![]()
則![]()
在![]() 中,
中,![]() ,即
,即
則![]() ;
;
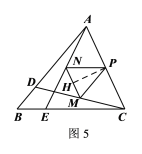
(3)依題意,分以下兩種情況:
①當(dāng)點(diǎn)D、E分別是邊AB、CB上的動點(diǎn)時
如圖6,作![]() 的角平分線交AB邊于點(diǎn)F,并連結(jié)BP
的角平分線交AB邊于點(diǎn)F,并連結(jié)BP
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,即
,即![]()
設(shè)![]() ,則
,則![]()
![]()
解得![]() 或
或![]() (不符題意,舍去)
(不符題意,舍去)
即![]()
![]()
由(2)可知,![]()
![]()
![]() 點(diǎn)P是AC上的中點(diǎn)
點(diǎn)P是AC上的中點(diǎn)
![]() ,
,![]() (等腰三角形的三線合一)
(等腰三角形的三線合一)
在![]() 中,
中,![]() ,即
,即![]()
![]()
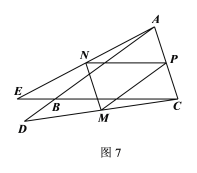
②如圖7,當(dāng)點(diǎn)D、E分別是邊AB、CB的延長線上的動點(diǎn)時
同理可得:![]()
![]()
![]()
綜上,MN的長為![]() 或
或![]() .
.




| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
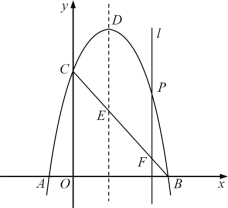
【題目】如圖,二次函數(shù)y=ax2+bx+4的圖象與x軸交于點(diǎn)A(-1,0),B(4,0),與y軸交于點(diǎn)C,拋物線的頂點(diǎn)為D,其對稱軸與線段BC交于點(diǎn)E.垂直于x軸的動直線l分別交拋物線和線段BC于點(diǎn)P和點(diǎn)F,動直線l在拋物線的對稱軸的右側(cè)(不含對稱軸)沿x軸正方向移動到B點(diǎn).
(1)求出二次函數(shù)y=ax2+bx+4和BC所在直線的表達(dá)式;
(2)在動直線l移動的過程中,試求使四邊形DEFP為平行四邊形的點(diǎn)P的坐標(biāo);
(3)連接CP,CD,在移動直線l移動的過程中,拋物線上是否存在點(diǎn)P,使得以點(diǎn)P,C,F為頂點(diǎn)的三角形與![]() DCE相似,如果存在,求出點(diǎn)P的坐標(biāo),如果不存在,請說明理由.
DCE相似,如果存在,求出點(diǎn)P的坐標(biāo),如果不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,菱形ABCD中,E,F分別是對角線BD和邊BC上一點(diǎn),且滿足∠EAF=∠ABD=![]() .
.
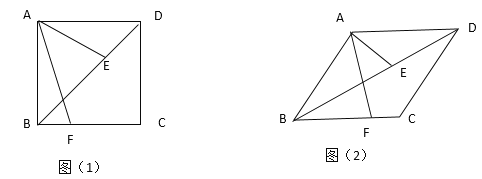
(1)如圖(1),當(dāng)![]() =45°時,求證:AF=
=45°時,求證:AF=![]() AE
AE
(2)如圖(2),探究AF與AE的數(shù)量關(guān)系(用含![]() 的銳角三角函數(shù)表示)
的銳角三角函數(shù)表示)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的圖像在第一象限有一個公共點(diǎn),其橫坐標(biāo)為1,則一次函數(shù)
的圖像在第一象限有一個公共點(diǎn),其橫坐標(biāo)為1,則一次函數(shù)![]() 的圖像可能是( )
的圖像可能是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】學(xué)生社團(tuán)是指學(xué)生在自愿基礎(chǔ)上結(jié)成的各種群眾性文化、藝術(shù)、學(xué)術(shù)團(tuán)體.不分年級、由興趣愛好相近的同學(xué)組成,在保證學(xué)生完成學(xué)習(xí)任務(wù)和不影響學(xué)校正常教學(xué)秩序的前提下開展各種活動.某校就學(xué)生對“籃球社團(tuán)、動漫社團(tuán)、文學(xué)社團(tuán)和攝影社團(tuán)”四個社團(tuán)選擇意向進(jìn)行了抽樣調(diào)查(每人選報一類),繪制了如圖所示的兩幅統(tǒng)計圖(不完整).

請根據(jù)圖中信息,解答下列問題:
(1)求扇形統(tǒng)計圖中m的值,并補(bǔ)全條形統(tǒng)計圖;
(2)在“動漫社團(tuán)”活動中,甲、乙、丙、丁、戊五名同學(xué)表現(xiàn)優(yōu)秀,現(xiàn)決定從這五名同學(xué)中任選兩名參加“中學(xué)生原創(chuàng)動漫大賽”,恰好選中甲、乙兩位同學(xué)的概率為 .
(3)已知該校有1200名學(xué)生,請估計“文學(xué)社團(tuán)”共有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校為獎勵在家自主學(xué)習(xí)有突出表現(xiàn)的學(xué)生,決定購買筆記本和鋼筆作為獎品.已知1本筆記本和4支鋼筆共需100元,4本筆記本和6支鋼筆共需190元.
(1)分別求一本筆記本和一支鋼筆的售價;
(2)若學(xué)校準(zhǔn)備購進(jìn)這兩種獎品共90份,并且筆記本的數(shù)量不多于鋼筆數(shù)量的3倍,請?jiān)O(shè)計出最省錢的購買方案,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某游泳館每年夏季推出兩種游泳付費(fèi)方式,方式一:先購買會員證,每張會員證100元,只限本人當(dāng)年使用,憑證游泳每次再付費(fèi)5元;方式二:不購買會員證,每次游泳付費(fèi)9元.
設(shè)小明計劃今年夏季游泳次數(shù)為x(x為正整數(shù)).
(I)根據(jù)題意,填寫下表:
游泳次數(shù) | 10 | 15 | 20 | … | x |
方式一的總費(fèi)用(元) | 150 | 175 | ______ | … | ______ |
方式二的總費(fèi)用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明計劃今年夏季游泳的總費(fèi)用為270元,選擇哪種付費(fèi)方式,他游泳的次數(shù)比較多?
(Ⅲ)當(dāng)x>20時,小明選擇哪種付費(fèi)方式更合算?并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩輛汽車沿同一公路從A地出發(fā)前往路程為100千米的B地,乙車比甲車晚出發(fā)15分鐘,行駛過程中所行駛的路程分別用y1、y2(千米)表示,它們與甲車行駛的時間x(分鐘)之間的函數(shù)關(guān)系如圖所示.
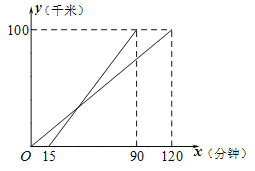
(1)分別求出y1、y2關(guān)于x的函數(shù)解析式并寫出定義域;
(2)乙車行駛多長時間追上甲車?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】四張質(zhì)地相同的卡片如圖所示.將卡片洗勻后,背面朝上放置在桌面上.
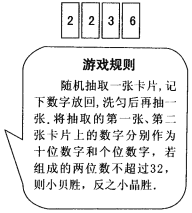
(1)求隨機(jī)抽取一張卡片,恰好得到數(shù)字2的概率;
(2)小貝和小晶想用以上四張卡片做游戲,游戲規(guī)則見信息圖.你認(rèn)為這個游戲公平嗎?請用列表法或畫樹形圖法說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com