
【題目】如圖,在△ABC中,∠ABC的平分線交AC于點D.作∠BDE=∠ABD交AB于點E.

(1)求證:ED∥BC;
(2)點M為射線AC上一點(不與點A重合)連接BM,∠ABM的平分線交射線ED于點N.若∠MBC=![]() ∠NBC,∠BED=105°,求∠ENB的度數.
∠NBC,∠BED=105°,求∠ENB的度數.
【答案】(1)見解析;(2)∠ENB的度數為50°或30°.
【解析】
(1)利用角平分線的定義,進行等量代換,得出內錯角相等,從而兩直線平行;
(2)分兩種情況分別進行解答,根據每一種情況畫出相應的圖形,依據圖形中,角之間的相互關系,轉化到一個三角形中,利用三角形的內角和定理,設未知數,列方程求解即可.
(1)∵BD平分∠ABC,
∴∠ABD=∠DBC,
又∵∠BDE=∠ABD,
∴∠BDE=∠DBC,
∴ED∥BC;
(2)∵BN平分∠ABM,
∴∠ABN=∠NBM,
①當點M在線段AC上時,如圖1所示:
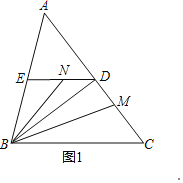
∵DE∥BC,
∴∠ENB=∠NBC,
∵∠MBC=![]() ∠NBC,
∠NBC,
∴∠NBM=∠MBC=![]() ∠NBC,
∠NBC,
設∠MBC=x°,則∠EBN=∠NBM=x°,∠ENB=∠NBC=2x°,
在△ENB中,由內角和定理得:x+2x+105°=180°,
解得:x=25,
∴∠ENB=2x=50°,
②當點M在AC的延長線上時,如圖2所示:
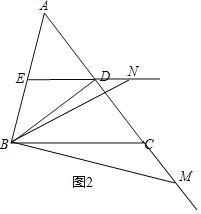
∵DE∥BC,
∴∠ENB=∠NBC,
∵∠MBC=![]() ∠NBC,
∠NBC,
∴∠NBM=3∠MBC,
設∠MBC=x°,則∠EBN=∠NBM=3x°,∠ENB=∠NBC=2x°,
在△EMB中,由內角和定理得:3x+2x+105°=180°,
解得:x=15,
∴∠ENB=2x=30°,
答:∠ENB的度數為50°或30°.


科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象交x軸于A(﹣1,0)、B(2,0)兩點,交y軸于點C(0,﹣2),過點A、C畫直線.
(1)求二次函數的解析式;
(2)若點P在x軸正半軸上,且PA=PC,求OP的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 分別是三角形
分別是三角形![]() 的邊
的邊![]() 的中點,
的中點,![]() 是
是![]() 所在平面上的動點,連接
所在平面上的動點,連接![]() ,點
,點![]() 分別是
分別是![]() 的中點,順次連接點
的中點,順次連接點![]()

(1)如圖,當點![]() 在
在![]() 的內部時,求證:四邊形
的內部時,求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)若四邊形![]() 是菱形,則
是菱形,則![]() 與
與![]() 應滿足怎樣的關系?若四邊形
應滿足怎樣的關系?若四邊形![]() 是矩形,則
是矩形,則![]() 與
與![]() 應滿足怎樣的關系?(直接寫出答案,不需要說明理由)
應滿足怎樣的關系?(直接寫出答案,不需要說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2-(2k+3)x+k2=0有兩個不相等的實數根x1,x2.
(1)求k的取值范圍;
(2)若兩不相等的實數根滿足![]() -
-![]() -
-![]() =-9,求實數k的值.
=-9,求實數k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市茶葉專賣店銷售某品牌茶葉,其進價為每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后來經過市場調查發現,單價每降低 10 元,則平均每周的銷售量可增加 40 千克,若該專賣店銷售這種品牌茶葉要想平均每周獲利 41600 元,請回答:
(1)每千克茶葉應降價多少元?
(2)在平均每周獲利不變的情況下,為盡可能讓利于顧客,贏得市場,該店應按原售價的 幾折出售?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)①如圖1,已知![]() ,
,![]() ,可得
,可得![]() __________.
__________.

②如圖2,在①的條件下,如果![]() 平分
平分![]() ,則
,則![]() __________.
__________.

③如圖3,在①、②的條件下,如果![]() ,則
,則![]() __________.
__________.
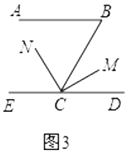
(2)嘗試解決下面問題:已知如圖4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分線,
的平分線,![]() ,求
,求![]() 的度數.
的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1是一個長為4a、寬為b的長方形,沿圖中虛線用剪刀平均分成四塊小長方形,然后用四塊小長方形拼成的一個“回形”正方形(如圖2).

(1)圖2中的陰影部分的面積為 ;
(2)觀察圖2請你寫出(a+b)2、(ab)2、ab之間的等量關系是 ;
(3)根據(2)中的結論,若m+n=5,mn=4,則mn= ;
(4)實際上通過計算圖形的面積可以探求相應的等式.根據圖3,寫出一個因式分解的等 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=AC,∠A=36°,AB的垂直平分線MN交AB于點M,交AC于點D,下列結論:①△BCD是等腰三角形;②BD是∠ABC的平分線;③DC+BC=AB;④△AMD≌△BCD,正確的是 ( )

A.①②B.②③C.①②③D.①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“五一勞動節大酬賓!”,某商場設計的促銷活動如下:在一個不透明的箱子里放有4個相同的小球,球上分別標有“0元”、“10元”、“20元”和“50元”的字樣.規定:在本商場同一日內,顧客每消費滿300元,就可以在箱子里先后摸出兩個球(第一次摸出后不放回).商場根據兩小球所標金額的和返還相等價格的購物券,購物券可以在本商場消費.某顧客剛好消費300元.
(1)該顧客至多可得到 元購物券;
(2)請你用畫樹狀圖或列表的方法,求出該顧客所獲得購物券的金額不低于50元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com