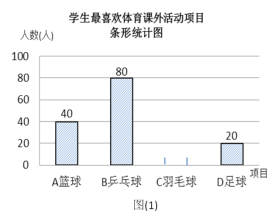
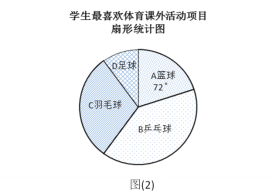
【題目】某學校為了豐富學生課余生活，決定開設以下體育課外活動項目：A籃球；B乒乓球；C羽毛球；D足球，為了解學生最喜歡哪一種活動項目，隨機抽取了部分學生進行調查，并將調查結果繪制成了兩幅不完整的統計圖，請回答下列問題：
(1)這次被調查的學生共有__________人；
(2)請你將條形統計圖(1)補充完整；
(3)在平時的乒乓球項目訓練中，甲、乙、丙、丁四人表現優秀，現決定從這四名同學中任選兩名參加乒乓球比賽，求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答)
鷹派教輔銜接教材河北教育出版社系列答案
初中暑期銜接系列答案科目：初中數學 來源： 題型：
【題目】某學校為了解九年級男同學1000米跑步的成績，隨機抽取了部分男生進行測試，并將測試成績分為A、B、C、D四個等級，繪制了不完整的成績等級頻數表和扇形統計圖．
成績等級 | 頻數 |
A | 24 |
B | 10 |
C | b |
D | 2 |
合計 | a |
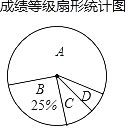
（1）表中a＝ ，b＝ ；
（2）扇形圖中C的圓心角度數是 ；
（3）若該校共有九年級男生600人，請估計沒有獲得A等級的學生人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一個矩形紙片OACB，將該紙片放置在平面直角坐標系中，點A（11，0），點B（0，6），點P為BC邊上的動點（點P不與點B、C重合），經過點O、P折疊該紙片，得點B′和折痕OP．設BP=t．
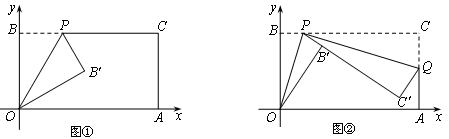
（Ⅰ）如圖①，當∠BOP=300時，求點P的坐標；
（Ⅱ）如圖②，經過點P再次折疊紙片，使點C落在直線PB′上，得點C′和折痕PQ，若AQ=m，試用含有t的式子表示m；
（Ⅲ）在（Ⅱ）的條件下，當點C′恰好落在邊OA上時，求點P的坐標（直接寫出結果即可）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解某校九年級學生課堂發言情況，隨機抽取該年級部分學生，對他們某天在課堂上發言的次數進行統計，結果如下表，并繪制了如下尚不完整的統計圖，已知
，
兩組發言的人數比為5：2，請結合圖表中相關數據回答下列問題：
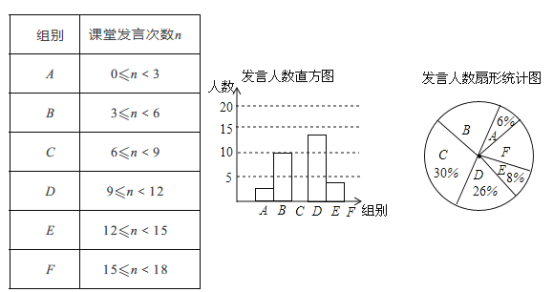
（1）本次抽樣的學生人數為_________；
（2）補全條形統計圖；
（3）該年級共有學生500人，請估計這天全年級發言次數不少于12的人數；
（4）已知
組發言的學生中有1位女生，組發言的學生中有2位男生，現從組與組中分別抽一位學生寫報告，請用樹狀圖或列表法，求所抽到的兩位學生恰好是一男一女的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD中，AB＝3，BC＝4，點E是A邊上一點，且AE＝
，點F是邊BC上的任意一點，把△BEF沿EF翻折，點B的對應點為G，連接AG，CG，則四邊形AGCD的面積的最小值為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把一張寬為1cm的長方形紙片ABCD折疊成如圖所示的陰影圖案，頂點A，D互相重合，中間空白部分是以E為直角頂點，腰長為2cm的等腰直角三角形，則紙片的長AD（單位：cm）為（ ）
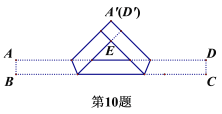
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用各種盛水容器可以制作精致的家用流水景觀（如圖1）．
科學原理：如圖2，始終盛滿水的圓體水桶水面離地面的高度為H（單位：m），如果在離水面豎直距離為h（單校：cm）的地方開大小合適的小孔，那么從小孔射出水的射程（水流落地點離小孔的水平距離）s（單位：cm）與h的關系為s2=4h（H—h）．
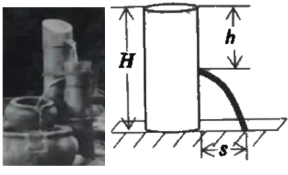
應用思考：現用高度為20cm的圓柱體望料水瓶做相關研究，水瓶直立地面，通過連注水保證它始終盛滿水，在離水面豎直距高h cm處開一個小孔．
（1）寫出s2與h的關系式；并求出當h為何值時，射程s有最大值，最大射程是多少?
（2）在側面開兩個小孔，這兩個小孔離水面的豎直距離分別為a，b，要使兩孔射出水的射程相同，求a，b之間的關系式；
（3）如果想通過墊高塑料水瓶，使射出水的最大射程增加16cm，求整高的高度及小孔離水面的豎直距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
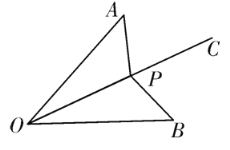
【題目】如圖，已知射線OC為∠AOB的平分線，且OA＝OB，點P是射線OC上的任意一點，連接AP、BP．
（1）求證：△AOP≌△BOP；
（2）若∠AOB＝50°，且點P是△AOB的外心，求∠APB的度數；
（3）若∠AOB＝50°，且△OAP為鈍角三角形，直接寫出∠OAP的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了慶祝中華人民共和國成立70周年，某市決定開展“我和祖國共成長”主題演講比賽，某中學將參加本校選拔賽的40名選手的成績(滿分為100分，得分為正整數且無滿分，最低為75分)分成五組，并繪制了下列不完整的統計圖表.
分數段 | 頻數 | 頻率 |
74.5～79.5 | 2 | 0.05 |
79.5～84.5 | m | 0.2 |
84.5～89.5 | 12 | 0.3 |
89.5～94.5 | 14 | n |
94.5～99.5 | 4 | 0.1 |
(1)表中m＝__________，n＝____________；
(2)請在圖中補全頻數直方圖；
(3)甲同學的比賽成績是40位參賽選手成績的中位數，據此推測他的成績落在_________分數段內；
(4)選拔賽中，成績在94.5分以上的選手，男生和女生各占一半，學校從中隨機確定2名選手參加全市決賽，請用列舉法或樹狀圖法求恰好是一名男生和一名女生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
