
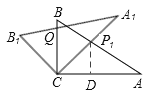
【題目】(2013年四川自貢12分)將兩塊全等的三角板如圖①擺放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.

(1)將圖①中的△A1B1C順時針旋轉45°得圖②,點P1是A1C與AB的交點,點Q是A1B1與BC的交點,求證:CP1=CQ;
(2)在圖②中,若AP1=2,則CQ等于多少?
(3)如圖③,在B1C上取一點E,連接BE、P1E,設BC=1,當BE⊥P1B時,求△P1BE面積的最大值.
【答案】解答:(1)證明:∵∠B1CB=45°,∠B1CA1=90°,∴∠B1CQ=∠BCP1=45°。
∵在△B1CQ和△BCP1中, ,
,
∴△B1CQ≌△BCP1(ASA)。∴CQ=CP1。
(2)如圖,過點P1作P1D⊥CA于D,
∵∠A=30°,∴P1D=![]() AP1=1。
AP1=1。
∵∠P1CD=45°,∴![]() 。.
。.
∴CP1=![]() P1D=
P1D=![]() 。
。
又∵CP1=CQ,∴CQ=![]() 。
。
(3)∵∠P1BE=90°,∠ABC=60°,∴∠A=∠CBE=30°。∴AC=、![]() BC 。
BC 。
由旋轉的性質可得:∠ACP1=∠BCE,∴△AP1C∽△BEC。∴AP1:BE=AC:BC=![]() :1。
:1。
設AP1=x,則BE=![]() x,
x,
在Rt△ABC中,∠A=30°,∴AB=2BC=2。
∴![]() 。
。
∵![]() ,∴當x=1時,S△P1BE(max)=
,∴當x=1時,S△P1BE(max)=![]() 。
。
【解析】(1)先判斷∠B1CQ=∠BCP1=45°,利用ASA即可證明△B1CQ≌△BCP1,從而得出結論。
(2)過點P1作P1D⊥CA于D,在RtADP1中,求出P1D,在Rt△CDP1中求出CP1,繼而可得出CQ的長度。
(3)證明△AP1C∽△BEC,則有AP1:BE=AC:BC=![]() :1,設AP1=x,則BE=
:1,設AP1=x,則BE=![]() x,得出S△P1BE關于x的表達式,利用配方法求最值即可。
x,得出S△P1BE關于x的表達式,利用配方法求最值即可。


科目:初中數學 來源: 題型:
【題目】如圖, 在8×8的正方形網格中,△ABC的頂點在邊長為1的小正方形的頂點上
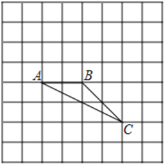
(1) 填空∠ABC=___________
(2) 若點A在網格所在的坐標平面內的坐標為(1,-2),請建立平面直角坐標系,D是平面直角坐標系中一點,并作出以A、B、C、D四個點為頂點的平行四邊形,直接寫出滿足條件的D點的坐標
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,對稱軸為直線![]() 的拋物線
的拋物線![]() 與x軸相交于A、B兩點,其中A點的坐標為(-3,0)。
與x軸相交于A、B兩點,其中A點的坐標為(-3,0)。

(1)求點B的坐標;
(2)已知![]() ,C為拋物線與y軸的交點。
,C為拋物線與y軸的交點。
①若點P在拋物線上,且![]() ,求點P的坐標;
,求點P的坐標;
②設點Q是線段AC上的動點,作QD⊥x軸交拋物線于點D,求線段QD長度的最大值。
查看答案和解析>>
科目:初中數學 來源: 題型:
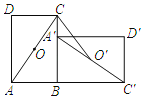
【題目】如圖,在矩形ABCD中,O是對角線AC的中點.將ABCD繞點B順時針旋轉90°.旋轉后的四邊形為A'B′C′D',點A,C,D,O的對應點分別為A′,C',D',O’,若AB=8,BC=10,則線段CO’的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求作圖
在下面的網格中,已知△ABC的頂點分別落在網格的格點,點A′、C′分別是點A、C兩點繞某一點O旋轉同樣的角度后的對應點.
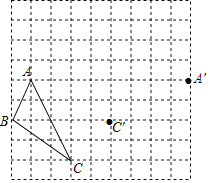
(1)請在下圖中作出旋轉中心O的位置;
(2)點A′是點A繞點O旋轉 度形成的;
(3)畫出△ABC繞點O旋轉同樣的角度后的△A′B'C’.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=105°,AC邊上的垂直平分線交AB邊于點D,交AC邊于點E,連結CD.
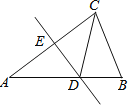
(1)若AB=10,BC=6,求△BCD的周長;
(2)若AD=BC,試求∠A的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b(k、b為常數,k≠0)的圖象與x軸、y軸分別交于A、B兩點,且與反比例函數y=![]() (n為常數,且n≠0)的圖象在第二象限交于點C.CD⊥x軸,垂足為D,若OB=2OA=3OD=12.
(n為常數,且n≠0)的圖象在第二象限交于點C.CD⊥x軸,垂足為D,若OB=2OA=3OD=12.
(1)求一次函數與反比例函數的解析式;
(2)記兩函數圖象的另一個交點為E,求△CDE的面積;
(3)直接寫出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小華和小麗設計了A、B兩種游戲:游戲A的規則是:用3張數字分別是2、3、4的撲克牌,將牌洗勻后背面朝上放置在桌面上,第一次隨機抽出一張牌記下數字后再原樣放回,洗勻后再第二次隨機抽出一張牌記下數字,若抽出的兩張牌上的數字之和為偶數,則小華獲勝;若兩數字之和為奇數,則小麗獲勝.游戲B的規則是:用4張數字分別是5、6、8、8的撲克牌,將牌洗勻后背面朝上放置在桌面上,小華先隨機抽出一張牌,抽出的牌不放回,小麗從剩下的牌中再隨機抽出一張牌,若小華抽出的牌面上的數字比小麗抽出的牌面上的數字大,則小華獲勝,否則小麗獲勝.請你幫小麗選擇其中一種游戲,使她獲勝的可能性較大,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com