
【題目】(感知)如圖1,在平面直角坐標(biāo)系中,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,將線段
,將線段![]() 繞著點(diǎn)
繞著點(diǎn)![]() 按逆時針方向旋轉(zhuǎn)
按逆時針方向旋轉(zhuǎn)![]() 至線段
至線段![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸,垂足為點(diǎn)
軸,垂足為點(diǎn)![]() ,易知
,易知![]() ,得到點(diǎn)
,得到點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
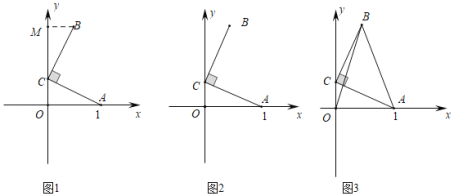
(探究)如圖2,在平面直角坐標(biāo)系中,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,將線段
,將線段![]() 繞著點(diǎn)
繞著點(diǎn)![]() 按逆時針方向旋轉(zhuǎn)
按逆時針方向旋轉(zhuǎn)![]() 至線段
至線段![]() .
.
(1)求點(diǎn)![]() 的坐標(biāo).(用含
的坐標(biāo).(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(2)求出BC所在直線的函數(shù)表達(dá)式.
(拓展)如圖3,在平面直角坐標(biāo)系中,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 軸上,將線段
軸上,將線段![]() 繞著點(diǎn)
繞著點(diǎn)![]() 按逆時針方向旋轉(zhuǎn)
按逆時針方向旋轉(zhuǎn)![]() 至線段
至線段![]() ,連結(jié)
,連結(jié)![]() 、
、![]() ,則
,則![]() 的最小值為_______.
的最小值為_______.
【答案】【探究】(1)點(diǎn)![]() 坐標(biāo)為
坐標(biāo)為![]() ;(2)
;(2)![]() ;【拓展】
;【拓展】![]() .
.
【解析】
探究:(1)證明△AOC≌△CMB(AAS),即可求解;
(2)根據(jù)點(diǎn)B的坐標(biāo)為(m,m+1),點(diǎn)![]() 坐標(biāo)
坐標(biāo)![]() ,即可求解;
,即可求解;
拓展:BO+BA=![]() ,BO+BA的值,相當(dāng)于求點(diǎn)P(m,m)到點(diǎn)M(1,-1)和點(diǎn)N(0,-1)的最小值,即可求解.
,BO+BA的值,相當(dāng)于求點(diǎn)P(m,m)到點(diǎn)M(1,-1)和點(diǎn)N(0,-1)的最小值,即可求解.
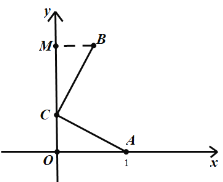
解:探究:(1)過點(diǎn)![]() 作
作![]() 軸,垂足為點(diǎn)
軸,垂足為點(diǎn)![]() .
.
![]() ,
,
![]() .
.
![]() 線段
線段![]() 繞著點(diǎn)
繞著點(diǎn)![]() 按逆時針方向旋轉(zhuǎn)
按逆時針方向旋轉(zhuǎn)![]() 至線段
至線段![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() 點(diǎn)
點(diǎn)![]() 坐標(biāo)
坐標(biāo)![]() ,點(diǎn)
,點(diǎn)![]() 坐標(biāo)
坐標(biāo)![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 坐標(biāo)為
坐標(biāo)為![]()
(2)∵點(diǎn)B的坐標(biāo)為(m,m+1),點(diǎn)C為(0,m),
設(shè)直線BC為:y=kx+b,
![]() ,解得:
,解得: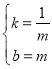 ,
,
∴![]() ;
;
則BC所在的直線為:![]() ;
;
拓展:如圖作BH⊥OH于H.
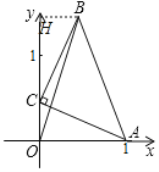
設(shè)點(diǎn)C的坐標(biāo)為(0,m),
由(1)知:OC=HB=m,OA=HC=1,
則點(diǎn)B(m,1+m),
則:BO+BA=![]() ,
,
BO+BA的值,相當(dāng)于求點(diǎn)P(m,m)到點(diǎn)M(1,-1)和點(diǎn)N(0,-1)的最小值,
相當(dāng)于在直線y=x上尋找一點(diǎn)P(m,m),使得點(diǎn)P到M(0,-1),到N(1,-1)的距離和最小,
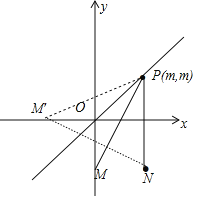
作M關(guān)于直線y=x的對稱點(diǎn)M′(-1,0),
易知PM+PN=PM′+PN≥NM′,
M′N=![]() ,
,
故:BO+BA的最小值為![]() ,
,
故答案為:![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
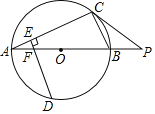
【題目】如圖,AB為⊙O的直徑,點(diǎn)P在AB的延長線上,點(diǎn)C在⊙O上,且PC2=PBPA.
(1)求證:PC是⊙O的切線;
(2)已知PC=20,PB=10,點(diǎn)D是![]() 的中點(diǎn),DE⊥AC,垂足為E,DE交AB于點(diǎn)F,求EF的長.
的中點(diǎn),DE⊥AC,垂足為E,DE交AB于點(diǎn)F,求EF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖①,等邊三角形![]() 的邊長為2,
的邊長為2,![]() 是
是![]() 邊上的任一點(diǎn)(與
邊上的任一點(diǎn)(與![]() 不重合),設(shè)
不重合),設(shè)![]() ,連接
,連接![]() ,以
,以![]() 為邊向兩側(cè)作等邊三角形
為邊向兩側(cè)作等邊三角形![]() 和等邊三角形
和等邊三角形![]() ,分別與邊
,分別與邊![]() 交于點(diǎn)
交于點(diǎn)![]() .
.
(1)求證:![]() ;
;
(2)求四邊形![]() 與△ABC重疊部分的面積
與△ABC重疊部分的面積![]() 與
與![]() 之間的函數(shù)關(guān)系式及
之間的函數(shù)關(guān)系式及![]() 的最小值;
的最小值;
(3)如圖②,連接![]() ,分別與邊
,分別與邊![]() 交于點(diǎn)
交于點(diǎn)![]() .當(dāng)
.當(dāng)![]() 為何值時,
為何值時,![]() .
.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
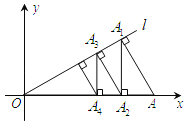
【題目】如圖,過點(diǎn)![]() 作直線
作直線![]() 的垂線,垂足為點(diǎn)
的垂線,垂足為點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸,垂足為點(diǎn)
軸,垂足為點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() …,這樣依次下去,得到一組線段
…,這樣依次下去,得到一組線段![]() …,則線段
…,則線段![]() 的長為__________.
的長為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,
,![]() ,直線
,直線![]() :
:![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,且與拋物線交于
,且與拋物線交于![]() ,
,![]() 兩點(diǎn),
兩點(diǎn),![]() 為拋物線上一動點(diǎn)(不與
為拋物線上一動點(diǎn)(不與![]() ,
,![]() 重合).
重合).
(1)求拋物線的解析式;
(2)當(dāng)點(diǎn)![]() 在直線
在直線![]() 下方時,過點(diǎn)
下方時,過點(diǎn)![]() 作
作![]() 軸交
軸交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 軸交
軸交![]() 于點(diǎn)
于點(diǎn)![]() ,求
,求![]() 的最大值.
的最大值.
(3)設(shè)![]() 為直線
為直線![]() 上的點(diǎn),以
上的點(diǎn),以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點(diǎn)的四邊形能否構(gòu)成平行四邊形?若能,求出點(diǎn)
為頂點(diǎn)的四邊形能否構(gòu)成平行四邊形?若能,求出點(diǎn)![]() 的坐標(biāo);若不能,請說明理由.
的坐標(biāo);若不能,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
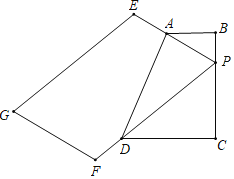
【題目】在四邊形ABCD中,AB∥CD,BC⊥CD,AB=2,CD=3,在BC上取點(diǎn)P(P與B、C不重合)連接PA延長至E,使PA=2AE,連接PD并延長至F,使PD=3FD,以PE、PF為邊作平行四邊形,另一個頂點(diǎn)為G,則PG長度的最小值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
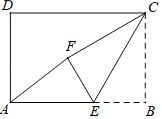
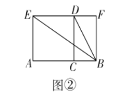
【題目】如圖,在矩形ABCD中,AB=3,CB=2,點(diǎn)E為線段AB上的動點(diǎn),將△CBE沿CE折疊,使點(diǎn)B落在矩形內(nèi)點(diǎn)F處,下列結(jié)論正確的是_____(寫出所有正確結(jié)論的序號)
①當(dāng)E為線段AB中點(diǎn)時,AF∥CE;
②當(dāng)E為線段AB中點(diǎn)時,AF=![]() ;
;
③當(dāng)A、F、C三點(diǎn)共線時,AE=![]() ;
;
④當(dāng)A、F、C三點(diǎn)共線時,△CEF≌△AEF.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
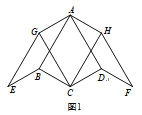
【題目】在四邊形 ABCD中,AB=AD,∠BAD=60°,邊BC繞點(diǎn)B順時針旋轉(zhuǎn)120°得到BE,邊DC繞點(diǎn)D逆時針旋轉(zhuǎn)120°得到DF,四邊形ABEG和四邊形ADFH為平行四邊形.
(1)如圖1,若BC=CD,∠BCD=120°,則∠GCH=_______°;
(2)如圖2,若BC≠CD,探究∠GCH的大小是否發(fā)生變化,并證明你的結(jié)論;
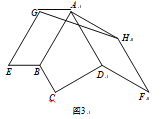
(3)如圖3,若∠BCD=∠ADC=90°,AB=![]() 請直接寫出△AGH的周長.
請直接寫出△AGH的周長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列材料,并完成相應(yīng)任務(wù):
黃金分割
天文學(xué)家開普勒把黃金分割稱為神圣分割,并指出畢達(dá)哥拉斯定理(勾股定理)和黃金分割是幾何中的雙寶,前者好比黃金,后者堪稱珠寶,歷史上最早正式在書中使用“黃金分割”這個名稱的是歐姆,19世紀(jì)以后“黃金分割”的說法逐漸流行起來,黃金分割被廣泛應(yīng)用于建筑等領(lǐng)域.黃金分割指把一條線段分為兩部分,使其中較長部分與線段總長之比等于較短部分與較長部分之比,該比值為![]() .用下面的方法(如圖①)就可以作出已知線段
.用下面的方法(如圖①)就可以作出已知線段![]() 的黃金分割點(diǎn)
的黃金分割點(diǎn)![]() :
:

①以線段![]() 為邊作正方形
為邊作正方形![]() ,
,
②取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() ,
,
③延長![]() 到
到![]() ,使
,使![]() ,
,
④以線段![]() 為邊作正方形
為邊作正方形![]() ,點(diǎn)
,點(diǎn)![]() 就是線段
就是線段![]() 的黃金分割點(diǎn).
的黃金分割點(diǎn).
以下是證明點(diǎn)![]() 就是線段
就是線段![]() 的黃金分割點(diǎn)的部分過程:
的黃金分割點(diǎn)的部分過程:
證明:設(shè)正方形![]() 的邊長為1,則
的邊長為1,則![]() ,
,
![]() 為
為![]() 中點(diǎn),
中點(diǎn),
![]() ,
,
![]() 在
在![]() 中,
中,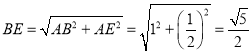 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任務(wù):
(1)補(bǔ)全題中的證明過程;
(2)如圖②,點(diǎn)![]() 為線段
為線段![]() 的黃金分割點(diǎn),分別以
的黃金分割點(diǎn),分別以![]() 為邊在線段
為邊在線段![]() 同側(cè)作正方形
同側(cè)作正方形![]() 和矩形
和矩形![]() ,連接
,連接![]() .求證:
.求證:![]() ;
;
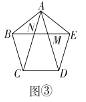
(3)如圖③,在正五邊形![]() 中,對角線
中,對角線![]() 與
與![]() 分別交于點(diǎn)
分別交于點(diǎn)![]() 求證:點(diǎn)
求證:點(diǎn)![]() 是
是![]() 的黃金分割點(diǎn).
的黃金分割點(diǎn).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com