【題目】某景區在同一線路上順次有三個景點A，B，C，甲、乙兩名游客從景點A出發，甲步行到景點C；乙花20分鐘時間排隊后乘觀光車先到景點B，在B處停留一段時間后，再步行到景點C．甲、乙兩人離景點A的路程s（米）關于時間t（分鐘）的函數圖像如圖所示．
（1）甲的速度是 米/分鐘；
（2）當20≤t ≤30時，求乙離景點A的路程s與t的函數表達式；
（3）乙出發后多長時間與甲在途中相遇？
（4）若當甲到達景點C時，乙與景點C的路程為360米，則乙從景點B步行到景點C的速度是多少？
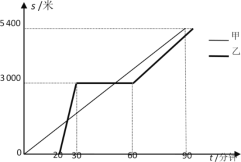
【答案】（1）60；（2）s＝300t－6000；（3）乙出發5分鐘和30分鐘時與甲在途中相遇；（4）乙從景點B步行到景點C的速度是68米/分鐘．
【解析】
（1）觀察圖像得出路程和時間，即可解決問題．
（2）利用待定系數法求一次函數解析式即可；
（3）分兩種情況討論即可；
（4）設乙從B步行到C的速度是x米/分鐘，根據當甲到達景點C時，乙與景點C的路程為360米，所用的時間為（90-60）分鐘，列方程求解即可．
（1）甲的速度為
60米/分鐘．
（2）當20≤t ≤30時，設s=mt＋n，由題意得：
，解得：
，所以s=300t－6000；
（3）①當20≤t ≤30時，60t=300t－6000，解得：t=25，25－20=5；
②當30≤t ≤60時，60t=3000，解得：t=50，50－20=30．
綜上所述：乙出發5分鐘和30分鐘時與甲在途中相遇．
（4）設乙從B步行到C的速度是x米/分鐘，由題意得：
5400－3000－（90－60） x=360
解得：x=68．
答：乙從景點B步行到景點C的速度是68米/分鐘．
高效智能課時作業系列答案
捷徑訓練檢測卷系列答案
小夫子全能檢測系列答案科目：初中數學 來源： 題型：
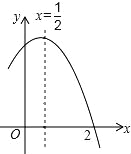
【題目】如圖是二次函數y=ax2+bx+c（a≠0）圖象的一部分，對稱軸為x=
，且經過點（2，0），有下列說法：①abc＜0；②a+b=0；③a﹣b+c=0；④若（0，y1），（1，y2）是拋物線上的兩點，則y1=y2．上述說法正確的是（ ）
A．①②③④ B．③④ C．①③④ D．①②
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知
是線段
上的任意一點（端點除外），分別以
，
為斜邊并且在的同一側作等腰直角
和
，連接
交
于點
，連接
交
于點
，給出以下三個結論：①
；②
；③
，其中正確結論的個數是（ ）
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB＝16，O為AB中點，點C在線段OB上（不與點O，B重合），將OC繞點O逆時針旋轉270°后得到扇形COD，AP，BQ分別切優弧
于點P，Q，且點P， Q在AB異側，連接OP．
（1）求證：AP＝BQ；
（2）當BQ＝4
時，求扇形COQ的面積及
的長（結果保留π）；
（3）若△APO的外心在扇形COD的內部，請直接寫出OC的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數的圖象與x軸相交于A（﹣3，0）、B（1，0）兩點，與y軸相交于點C（0，3），點C、D是二次函數圖象上的一對對稱點，一次函數的圖象過點B、D．
（1）求D點坐標；
（2）求二次函數的解析式；
（3）根據圖象直接寫出使一次函數值小于二次函數值的x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】矩形OABC的頂點A(-8，0)、C(0，6)，點D是BC邊上的中點，拋物線y=ax2+bx經過A、D兩點，如圖所示.
(1)求點D關于y軸的對稱點D′的坐標及a、b的值；
(2)在y軸上取一點P,使PA+PD長度最短,求點P的坐標；
(3)將拋物線y=ax2+bx向下平移,記平移后點A的對應點為A1，點D的對應點為D1，當拋物線平移到某個位置時，恰好使得點O是y軸上到A1、D1兩點距離之和OA1+OD1最短的一點，求此拋物線的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
