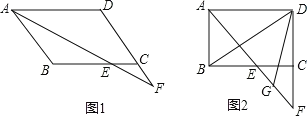
【題目】在ABCD中，∠BAD的平分線交直線BC于點E，交直線DC于點F．
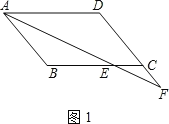
（1）在圖1中說明CE=CF；
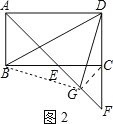
（2）若∠ABC=90°，G是EF的中點(如圖2)，求∠BDG的度數．
【答案】（1）答案見解析；（2）∠BDG=45°．
【解析】
（1）先根據角平分線的定義可得
，再根據平行四邊形的性質、平行線的性質可得
，從而可得
，然后根據等腰三角形的性質即可得證；
（2）先根據矩形的性質和題（1）的結論可得出
為等腰直角三角形，再根據等腰三角形的性質可得
，然后根據角平分線的定義、等腰三角形的判定與性質可得
，從而可得
，最后根據三角形全等的判定定理與性質可得
，從而可推出
為等腰直角三角形，由此即可得出答案．
（1）如圖1，AF平分
∵四邊形ABCD是平行四邊形
；
（2）如圖2，連接GC、BG
∵四邊形ABCD為平行四邊形，
∴四邊形ABCD為矩形
結合（1）的結論得，為等腰直角三角形
∵G為EF中點
（等腰三角形的三線合一）
又
AF平分，
為等腰直角三角形，
，即
在
與
中，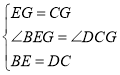
為等腰直角三角形
．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
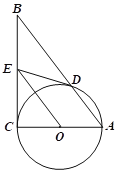
【題目】如圖在RtΔABC中，∠C=90°，以AC為直徑作⊙O，交AB于D，過O作OE∥AB，交BC于E．
（1）求證：ED是⊙O的切線；
（2）如果⊙O的半徑為1.5，ED=2，求AB的長．
（3）在（2）的條件下，求△ADO的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在一條東西走向河的一側有一村莊C，河邊原有兩個取水點A，B，其中AB＝AC，由于某種原因，由C到A的路現在已經不通，某村為方便村民取水決定在河邊新建一個取水點H（A、H、B在一條直線上），并新修一條路CH，測得CB＝3千米，CH＝2.4千米，HB＝1.8千米．
（1）問CH是否為從村莊C到河邊的最近路？（即問：CH與AB是否垂直？）請通過計算加以說明；
（2）求原來的路線AC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
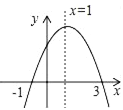
【題目】如圖為二次函數y=ax2+bx+c的圖象，給出下列說法：
①ab＞0；
②方程ax2+bx+c=0的根為x1=﹣1，x2=3；
③a+b+c＞0；
④當x＞1時，隨x值的增大而增大．
其中正確的說法有______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】解答下列各題
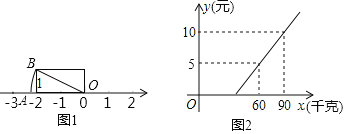
（1）如圖1，已知OA＝OB，數軸上的點A所表示的數為m，且|m+n|＝2
①點A所表示的數m為 ；
②求代數式n2+m﹣9的值．
（2）旅客乘車按規定可以隨身攜帶一定質量的行李，如果超過規定，則需購買行李票，設行李票y（元）是行李質量x（千克）的一次函數，其圖象如圖2所示．
①當旅客需要購買行李票時，求出y與x之間的函數關系式；
②如果張老師攜帶了42千克行李，她是否要購買行李票？如果購買需買多少行李票？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，點F從菱形ABCD的頂點A出發，沿A→D→B以1cm/s的速度勻速運動到點B，圖2是點F運動時，△FBC的面積y（cm2）隨時間x（s）變化的關系圖象，則a的值為（ ）
A. 
B. 2 C. 
D. 2
查看答案和解析>>
科目：初中數學 來源： 題型：
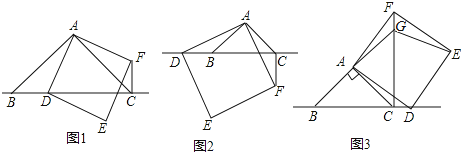
【題目】在△ABC中，∠BAC=90°，AB=AC，點D為直線BC上一動點（點D不與B，C重合），以AD為邊在AD右側作正方形ADEF，連接CF．
（1）觀察猜想
如圖1，當點D在線段BC上時，
①BC與CF的位置關系，
②BC，CD，CF之間的數量關系為；
（2）數學思考
如圖2，當點D在線段CB的延長線上時，結論①，②是否仍然成立？若成立，請給予證明；
若不成立，請你寫出正確結論再給予證明；
（3）拓展延伸
如圖3，當點D在線段BC的延長線上時，延長BA交CF于點G，連接GE．若已知AB=2
，CD=
BC，求CF，EG.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
