
【題目】對平面直角坐標系中的點P(x,y),定義d=|x|+|y|,我們稱d為P(x,y)的幸福指數.對于函數圖象上任意一點P(x,y),若它的幸福指數d≥1恒成立,則稱此函數為幸福函數,如二次函數y=x2+1就是一個幸福函數,理由如下:設P(x,y)為y=x2+1上任意一點,d=|x|+|y|=|x|+|x2+1|,∵|x|≥0,|x2+1|=x2+1≥1,∴d≥1.∴y=x2+1是一個幸福函數.
(1)若點P在反比例函數y=![]() 的圖象上,且它的幸福指數d=2,請直接寫出所有滿足條件的P點坐標;
的圖象上,且它的幸福指數d=2,請直接寫出所有滿足條件的P點坐標;
(2)一次函數y=﹣x+1是幸福函數嗎?請判斷并說明理由;
(3)若二次函數y=x2﹣(2m+1)x+m2+m(m>0)是幸福函數,試求出m的取值范圍.
【答案】(1)滿足條件的P點坐標為(﹣1,﹣1)或(1,1);
(2)一次函數y=﹣x+1是幸福函數,理由見解析;
(3)若二次函數y=x2﹣(2m+1)x+m2+m(m>0)是幸福函數,m的取值范圍為m≥2.
【解析】試題分析:(1)設點P的坐標為(m, ![]() ),根據幸福指數的定義,即可得出關于m的分式方程,解之經檢驗即可得出結論;
),根據幸福指數的定義,即可得出關于m的分式方程,解之經檢驗即可得出結論;
(2)設P(x,y)為y=-x+1上的一點,分x<0、0≤x≤1和x>1三種情況找出d的取值范圍,由此即可得出一次函數y=-x+1是幸福函數;
(3)設P(x,y)為y=x2-(2m+1)x+m2+m上的一點,由y=x2-(2m+1)x+m2+m=(x-m)(x-m-1)且m>0,可知分x≤0、0<x<m、m≤x≤m+1、x>m+1四段尋找m的取值范圍,利用配方法以及二次函數的性質結合幸福函數的定義即可求出m的取值范圍,綜上即可得出結論.
試題解析:
解:(1)設點P的坐標為(m, ![]() ),
),
∴d=|m|+|![]() |=2,
|=2,
解得:m1=﹣1,m2=1,
經檢驗,m1=﹣1,m2=1是原分式方程的解,
∴滿足條件的P點坐標為(﹣1,﹣1)或(1,1).
(2)一次函數y=﹣x+1是幸福函數,理由如下:
設P(x,y)為y=﹣x+1上的一點,d=|x|+|y|=|x|+|﹣x+1|,
當x<0時,d=|x|+|﹣x+1|=﹣x﹣x+1=1﹣2x>1;
當0≤x≤1時,d=|x|+|﹣x+1|=x﹣x+1=1;
當x>1時,d=|x|+|﹣x+1|=x+x﹣1=2x﹣1>1.
∴對于y=﹣x+1上任意一點P(x,y),它的幸福指數d≥1恒成立,
∴一次函數y=﹣x+1是幸福函數.
(3)設P(x,y)為y=x2-(2m+1)x+m2+m上的一點,d=|x|+|y|=|x|+|x2﹣(2m+1)x+m2+m|,
∵y=x2-(2m+1)x+m2+m=(x-m)(x-m-1),m>0,
∴分x≤0、0<x<m、m≤x≤m+1、x>m+1考慮.
①當x≤0時,d=|x|+|x2﹣(2m+1)x+m2+m|=﹣x+x2﹣(2m+1)x+m2+m=(x﹣m﹣1)2﹣m﹣1,
當x=0時,d取最小值,最小值為m2+m,
∴m2+m≥1,
解得:m≥![]() ;
;
②0<x<m時,d=|x|+|x2﹣(2m+1)x+m2+m|=x+x2﹣(2m+1)x+m2+m =(x﹣m)2+m﹣1≥1,
∵(x﹣m)2≥0,
∴m﹣1≥1,
解得:m≥2;
③當m≤x≤m+1時,d=|x|+|x2﹣(2m+1)x+m2+m|=x-x2+(2m+1)x-m2-m =﹣(x﹣m﹣1)2+m+1,
當x=m時,d取最小值,最小值為m,
∴m≥1;
④當x>m+1時,d=|x|+|x2﹣(2m+1)x+m2+m|=x+x2﹣(2m+1)x+m2+m=(x﹣m)2+m﹣1>m≥1,
∴m≥1.
綜上所述:若二次函數y=x2-(2m+1)x+m2+m(m>0)是幸福函數,m的取值范圍為m≥2.


科目:初中數學 來源: 題型:
【題目】已知四邊形ABCD是邊長為2的菱形,∠BAD=60°,對角線AC與BD交于點O,過點O的直線EF交AD于點E,交BC于點F.
(1)求證:△AOE≌△COF;
(2)若∠EOD=30°,求CE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() ,點
,點![]() 是線段
是線段![]() 上一點(不與端點
上一點(不與端點![]() 重合),
重合),![]() 、
、![]() 分別平分
分別平分![]() 和
和![]() 交
交![]() 于點
于點![]() 、
、![]() .
.
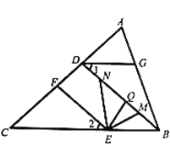
(1)請說明:![]() ;
;
(2)當點![]() 在
在![]() 上移動時,請寫出
上移動時,請寫出![]() 和
和![]() 之間滿足的數量關系為______;
之間滿足的數量關系為______;
(3)若![]() ,則當點
,則當點![]() 移動到使得
移動到使得![]() 時,請直接寫出
時,請直接寫出![]() ______(用含
______(用含![]() 的代數式表示).
的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查中,最適宜采用全面調查方式(普查)的是( )
A. 對襄陽市中學生每天課外讀書所用時間的調查
B. 對全國中學生心理健康現狀的調查
C. 對七年級(2)班學生![]() 米跑步成績的調查
米跑步成績的調查
D. 對市面某品牌中性筆筆芯使用壽命的調查
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,MN是⊙O的直徑,MN=2a,∠AMN=40°,點B為弧AN的中點,點P是直徑MN上的一個動點,則 PA+PB的最小值為_____.(用含a的代數式表示)
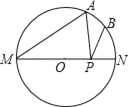
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC和△DBC都是邊長為2的等邊三角形.

(1)以圖1中的某個點為旋轉中心,旋轉△DBC,就能使△DBC與△ABC重合,則滿足題意的點為: (寫出符合條件的所有點);
(2)將△DBC沿BC方向平移得到△D1B1C1,如圖2、圖3,則四邊形ABD1C1是平行四邊形嗎?證明你的結論;
(3)在(2)的條件下,當BB1= 時,四邊形ABD1C1為矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
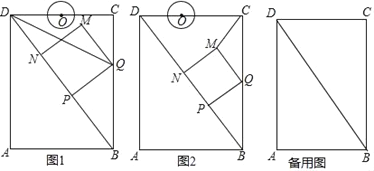
【題目】如圖,在矩形ABCD中,AB=6cm,AD=8cm,點P從點B出發,沿對角線BD向點D勻速運動,速度為4cm/s,過點P作PQ⊥BD交BC于點Q,以PQ為一邊作正方形PQMN,使得點N落在射線PD上.點O從點D出發,沿DC向點C勻速運動,速度為3cm/s,以O為圓心,1cm半徑作⊙O.點P與點D同時出發,設它們的運動時間為t(單位:s) (0≤t≤![]() ).
).
(1)如圖1,連接DQ,若DQ平分∠BDC,則t的值為 s;
(2)如圖2,連接CM,設△CMQ的面積為S,求S關于t的函數關系式;
(3)在運動過程中,當t為何值時,⊙O與MN第一次相切?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【探究證明】
(1)某班數學課題學習小組對矩形內兩條互相垂直的線段與矩形兩鄰邊的數量關系進行探究,提出下列問題,請你給出證明.
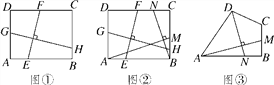
如圖①,在矩形ABCD中,EF⊥GH,EF分別交AB,CD于點E,F,GH分別交AD,BC于點G,H.求證: ![]() ;
;
【結論應用】
(2)如圖②,在滿足(1)的條件下,又AM⊥BN,點M,N分別在邊BC,CD上,若![]() ,則
,則![]() 的值為 ;
的值為 ;
【聯系拓展】
(3)如圖③,四邊形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,點M,N分別在邊BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com