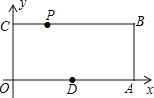
【題目】已知，如圖，O為坐標原點，四邊形OABC為矩形，A（10，0），C（0，4），點D是OA的中點，動點P在線段BC上以每秒2個單位長的速度由點C向B 運動．設 動點P的運動時間為t秒
（1）當t為何值時，四邊形PODB是平行四邊形？
（2）在直線CB上是否存在一點Q，使得O、D、Q、P四點為頂點的四邊形是菱形？若存在，求t的值,并求出Q點的坐標；若不存在，請說明理由。
（3) 在線段PB上有一點M，且PM=5，當P運動 秒時，四邊形OAMP的周長最小, 并畫圖標出點M的位置。
【答案】（1）t=2.5；（2）t=4 Q(3,4)；t=1 Q(-3,4)（3）t=
【解析】（1）根據平行四邊形的性質就可以知道PB=5，可以求出PC=5，從而可以求出t的值；（2）要使ODQP為菱形，可以得出PO=5，由三角形的勾股定理就可以求出CP的值而求出t的值；（3）根據題意即可填得t的值．
解： (1)∵四邊形PODB是平行四邊形，
∴PB=OD=5，
∴PC=5，
∴2t=5,t=2.5；
（2）當Q點在P的右邊時
∵四邊形ODQP為菱形，
∴OD=OP=PQ=5，
∴在Rt△OPC中，由勾股定理得：
PC=3，
∴2t=3；t=1.5 Q(8,4).
當Q點在P的左邊且在BC線段上時，t=4， Q(3,4)；
當Q點在P的左邊且在BC的延長線上時，t=1，Q(-3,4) ．
（3）t=．
“點睛”本題考查了平行四邊形的判定及性質，菱形的性質，勾股定理的運用，解題時要運用分類討論的思想．
海淀黃岡名師導航系列答案
普通高中同步練習冊系列答案科目：初中數學 來源： 題型：
【題目】如圖，拋物線 
與x軸的負半軸交于點A，與y軸交于點B，連結AB．點C 
在拋物線上，直線AC與y軸交于點D．
（1）求c的值及直線AC的函數表達式；
（2）點P在x軸的正半軸上，點Q在y軸正半軸上，連結PQ與直線AC交于點M，連結MO并延長交AB于點N，若M為PQ的中點．
①求證：△APM∽△AON；
②設點M的橫坐標為m ， 求AN的長（用含m的代數式表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市甲、乙兩個汽車銷售公司，去年一至十月份每月銷售同種品牌汽車的情況如圖所示：
請你根據上圖填寫下表：
銷售公司 | 平均數 | 方差 | 中位數 | 眾數 |
甲 |
| 9 | ||
乙 | 9 |
| 8 |
請你從以下兩個不同的方面對甲、乙兩個汽車銷售公司去年一至十月份的銷售情況進行分析：
從平均數和方差結合看；
從折線圖上甲、乙兩個汽車銷售公司銷售數量的趨勢看
分析哪個汽車銷售公司較有潛力
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知△ABC，△EFG均是邊長為4的等邊三角形，點D是邊BC、EF的中點． （Ⅰ）如圖①，這兩個等邊三角形的高為；
（Ⅱ）如圖②，直線AG，FC相交于點M，當△EFG繞點D旋轉時，線段BM長的最小值是 ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把下列各數填在相應的括號內
， -
, 0, 
,‐3.1415926, 20%, ‐3
, 2, -1，3.1010010001…（每兩個1之間逐次增加1個0）
①正數集合{ ……}
②負數集合{ ……}
③整數集合{ ……}
④負分數集合{ ……}
⑤無理數集合{ ……}
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，AB=4cm，∠ADC=120°，點E、F同時由A、C兩點出發，分別沿AB、CB方向向點B勻速移動（到點B為止），點E的速度為1cm/s，點F的速度為2cm/s，經過t秒△DEF為等邊三角形，則t的值為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，反比例函數y= 
（x＞0）的圖象經過矩形OABC對角線的交點M，分別與AB、BC相交于點D、E．若四邊形ODBE的面積為6，則k的值為 ．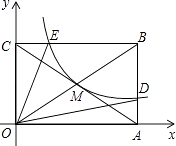 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學實驗室：
點A、B在數軸上分別表示有理數a、b，A、B兩點之間的距離表示為AB，在數軸上A、B兩點之間的距離AB=|a﹣b|．
利用數形結合思想回答下列問題：
（1）數軸上表示2和5的兩點之間的距離是_________，數軸上表示1和－3的兩點之間的距離是 ；
（2）數軸上若點A表示的數是x，點B表示的數是－2，則點A和B之間的距離是 ，若AB＝2，那么x為 ；
（3）當x是 時，代數式
；
（4）若點A表示的數－1，點B與點A的距離是10，且點B在點A的右側，動點P、Q同時從A、B出發沿數軸正方向運動，點P的速度是每秒3個單位長度，點Q的速度是每秒1個單位長度，求運動幾秒后，PQ＝1？（請寫出必要的求解過程）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
