
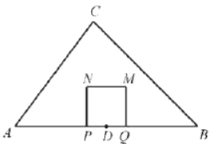
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 為
為![]() 中點.動點
中點.動點![]() 從點
從點![]() 出發,沿
出發,沿![]() 方向以每秒
方向以每秒![]() 個單位長度的速度向終點
個單位長度的速度向終點![]() 運動,點
運動,點![]() 關于點
關于點![]() 對稱點為點
對稱點為點![]() ,以
,以![]() 為邊向上作正方形
為邊向上作正方形![]() .設點
.設點![]() 的運動時間為
的運動時間為![]() 秒.
秒.
(1)當![]() _______秒時,點
_______秒時,點![]() 落在
落在![]() 邊上.
邊上.
(2)設正方形![]() 與
與![]() 重疊部分面積為
重疊部分面積為![]() ,當點
,當點![]() 在
在![]() 內部時,求
內部時,求![]() 關于
關于![]() 的函數關系式.
的函數關系式.
(3)當正方形![]() 的對角線所在直線將
的對角線所在直線將![]() 的分為面積相等的兩部分時,直接寫出
的分為面積相等的兩部分時,直接寫出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]() 的值為
的值為![]() 或
或![]() .
.
【解析】
(1)如下圖,根據![]() ,可得出PN與AP的關系,從而求出t的值;
,可得出PN與AP的關系,從而求出t的值;
(2)如下圖,存在2種情況,一種是點M在△ABC內,另一種是點M在△ABC外部,分別根據正方形和三角形求面積的公式可求解;
(3)如下圖,存在2種情況,一種是PM所在的直線將△ABC的面積平分,另一種是QN所在的直線將△ABC的面積平分.
(1)如圖1,點N在AC上
圖1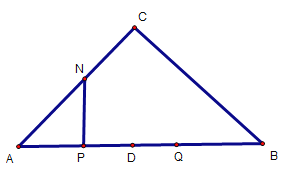
由題意可知:PD=DQ=t,AP=7-t
∴PN=PQ=2t
∵![]()
∴![]() ,即
,即![]()
解得:t=![]()
(2)①如圖2,
圖2
![]() 四邊形
四邊形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,即
,即![]()
解得![]() ,
,
故當![]() ≤
≤![]() 時,
時,![]() ;
;
②如圖3,
圖3
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
則![]() ,
,
![]() ,
,
![]() ,
,
則![]()
![]() ;
;
綜上, .
.
(3)如下圖,過點C作AB的垂線,交AB于點G
圖4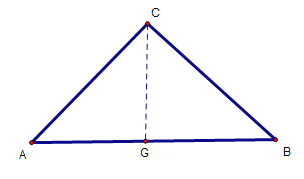
∵![]()
∴設CG=4x,則AG=3x
∵∠B=45°
∴△CBG是等腰直角三角形
∴GB=GC=4x
∵AB=14
∴3x+4x=14,解得:x=2
∴![]()
∴![]()
情況一:PM所在的直線平分△ABC的面積,如下圖,PM與BC交于點E
圖5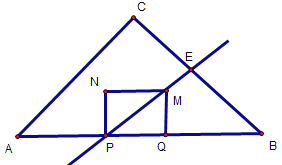
則![]()
∵四邊形PQMN是正方形,∴∠EPB=45°
∵∠B=45°
∴△PBE是等腰直角三角形
∵![]()
∴PE=PB=![]()
∴PB=![]()
∵PB=AB-PA=14-(7-t)=7+t
∴7+t=![]()
t=![]()
情況二:如下圖,QN所在線段平分△ABC的面積,QF交AC于點F,過點F作AB的垂線,交AB于點H
圖6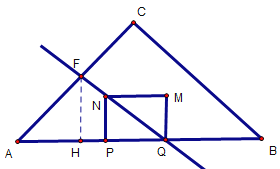
同理,![]()
∵四邊形PQMN是正方形,∴∠EQH=45°
∴△FHQ是等腰直角三角形
∵![]()
∴設FH=4y,則AH=3y,HQ=FH=4y,∴AQ=7y
∴![]() ,解得:y=
,解得:y=![]()
∵AQ=AB-QB=14-(7-t)=7+t
∴7+t=7![]()
解得:t=7![]()
∴綜上得:![]() 的值為
的值為![]() 或
或![]() .
.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
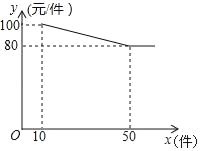
【題目】服裝廠批發某種服裝,每件成本為65元,規定不低于10件可以批發,其批發價y(元/件)與批發數量x(件)(x為正整數)之間所滿足的函數關系如圖所示.
(1)求y與x之間所滿足的函數關系式,并寫出x的取值范圍;
(2)設服裝廠所獲利潤為w(元),若10≤x≤50(x為正整數),求批發該種服裝多少件時,服裝廠獲得利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
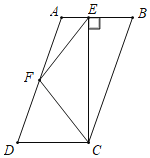
【題目】如圖,在ABCD中,AD=2AB,F是AD的中點,作CE⊥AB,垂足E在線段AB上,連接EF、CF,則下列結論中一定成立的是_____(把所有正確結論的序號部填在橫線上).①∠AEF=![]() ∠DFE;②S△BEC=2S△CEF;③EF=CF;④∠BCD=2∠DCF.
∠DFE;②S△BEC=2S△CEF;③EF=CF;④∠BCD=2∠DCF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是一個地鐵站入口的雙翼閘機.如圖2,它的雙翼展開時,雙翼邊緣的端點A與B之間的距離為10cm,雙翼的邊緣AC=BD=54cm,且與閘機側立面夾角∠PCA=∠BDQ=30°.當雙翼收起時,可以通過閘機的物體的最大寬度為( )
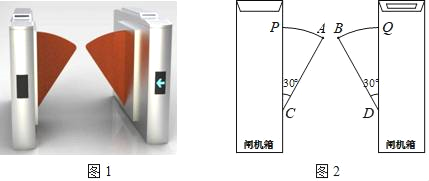
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與反比例函數
與反比例函數![]() 的圖象交于點
的圖象交于點![]() 和點
和點![]() .
.
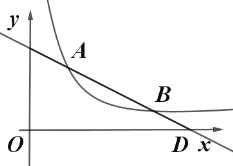
(1)求直線和反比例函數的解析式;
(2)若直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,嘉淇認為
,嘉淇認為![]() ,請通過計算說明她的觀點是否正確.
,請通過計算說明她的觀點是否正確.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家自2016年1月1日起實行全面放開二胎政策,某計生組織為了解該市家庭對待這項政策的態度,準備采用以下調查方式中的一種進行調查:
A.從一個社區隨機選取1 000戶家庭調查;
B.從一個城鎮的不同住宅樓中隨機選取1 000戶家庭調查;
C.從該市公安局戶籍管理處隨機抽取1 000戶城鄉家庭調查.
(1)在上述調查方式中,你認為比較合理的一個是【1】.(填“A”、“B”或“C”)
(2)將一種比較合理的調查方式調查得到的結果分為四類:(A)已有兩個孩子;
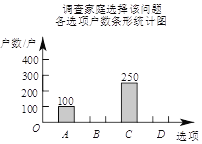
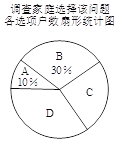
(B)決定生二胎;(C)考慮之中;(D)決定不生二胎.將調查結果繪制成如下兩幅不完整的統計圖.
請根據以上不完整的統計圖提供的信息,解答下列問題:
①補全條形統計圖.
②估計該市100萬戶家庭中決定不生二胎的家庭數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 為等邊
為等邊![]() 的高,
的高,![]() ,點P為直線
,點P為直線![]() 上的動點(不與點B重合),連接
上的動點(不與點B重合),連接![]() ,將線段
,將線段![]() 繞點P逆時針旋轉60°,得到線段
繞點P逆時針旋轉60°,得到線段![]() ,連接
,連接![]() 、
、![]() .
.
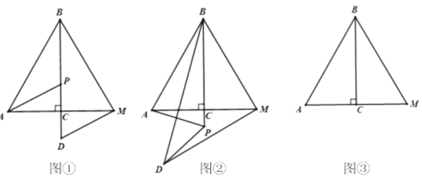
(1)問題發現:如圖①,當點D在直線![]() 上時,線段
上時,線段![]() 與
與![]() 的數量關系為_________,
的數量關系為_________,![]() _________;
_________;
(2)拓展探究:如圖②,當點P在![]() 的延長線上時,(1)中結論是否成立?若成立,請加以證明;若不成立,請說明理由;
的延長線上時,(1)中結論是否成立?若成立,請加以證明;若不成立,請說明理由;
(3)問題解決:當![]() 時,請直接寫出線段
時,請直接寫出線段![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點P是AB上一動點(不與A,B重合),對角線AC、BD相交于點O,過點P分別作AC、BD的垂線,分別交AC、BD于點E、F,交AD、BC于點M、N.下列結論:①△APE≌△AME;②PM+PN=AC;③△POF∽△BNF;④當△PMN∽△AMP時,點P是AB的中點,其中一定正確的結論有_____.(填上所有正確的序號).
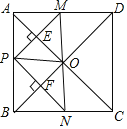
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com