
【題目】某市自來水公司為鼓勵居民節約用水,采取按月用水量分段收費的辦法,若某戶居民應交水費y(元)與用水量x(噸)的函數關系如圖所示.
(1)分別寫出當0≤x≤15和x≥15時,y與x的函數關系式;
(2)若某用戶該月應交水費42元,則該月用水多少噸?

【答案】(1) 當0≤x≤15時,y=![]() x;當x≥15時,y=2.5x﹣10.5;(2) 21噸.
x;當x≥15時,y=2.5x﹣10.5;(2) 21噸.
【解析】
試題分析:(1)先根據待定系數法求得OA和AB的解析式;
(2)再將y=42代入AB的解析式求解即可.
試題解析:(1)當0≤x≤15時,OA過點(0,0),(15,27),
設y=kx,
∴27=15k,
∴k=![]() ,
,
∴y=![]() x(0≤x≤15);
x(0≤x≤15);
當x≥15時,AB過點A(15,27),B(20,39.5),
設y=![]() x+b,
x+b,
則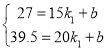 ,解得
,解得![]() ,
,
∴y=2.5x﹣10.5(x≥15),
綜上所述,當0≤x≤15時,y=![]() x;當x≥15時,y=2.5x﹣10.5;
x;當x≥15時,y=2.5x﹣10.5;
(2)∵42>27,
∴令y=42,則42=2.5x﹣10.5,
解得x=21,
故該月用水21噸.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
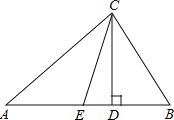
【題目】如圖,在△ABC中,CD、CE分別是△ABC的高和角平分線.
(1)若∠A=30°,∠B=50°,求∠ECD的度數;
(2)試用含有∠A、∠B的代數式表示∠ECD(不必證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】公司投資750萬元,成功研制出一種市場需求量較大的產品,并再投入資金1750萬元進行相關生產設備的改進.已知生產過程中,每件產品的成本為60元.在銷售過程中發現,當銷售單價定為120元時,年銷售量為24萬件;銷售單價每增加10元,年銷售量將減少1萬件.設銷售單價為x(元)(x>120),年銷售量為y(萬件),第一年年獲利(年獲利=年銷售額﹣生產成本)為z(萬元).
(1)求出y與x之間,z與x之間的函數關系式;
(2)該公司能否在第一年收回投資.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com