
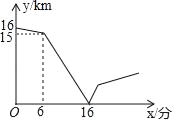
【題目】甲、乙兩人在一條筆直的道路上相向而行,甲騎自行車從A地到B地,乙駕車從B地到A地,他們分別以不同的速度勻速行駛,已知甲先出發6分鐘后,乙才出發,在整個過程中,甲、乙兩人的距離y(km)與甲出發的時間x(分)之間的關系如圖所示.
(1)求甲、乙相遇時,乙所行駛的路程;
(2)當乙到達終點A時,甲還需多少分鐘到達終點B?
【答案】(1)![]() 千米;(2)78分鐘.
千米;(2)78分鐘.
【解析】
(1)根據路程與時間的關系,可得甲、乙的速度,再根據甲、乙相遇時,乙所行駛的路程=10×乙的速度,即可解答;(2)根據相遇前甲行駛的路程除以乙行駛的速度,可得乙到達A站需要的時間,根據相遇前乙行駛的路程除以甲行駛的速度,可得甲到達B站需要的時間,再根據有理數的減法,可得結果.
(1)由縱坐標看出甲先行駛了1千米,由橫坐標看出甲行駛1千米用了6分鐘,
甲的速度是1÷6=![]() 千米/分鐘,
千米/分鐘,
由縱坐標看出AB兩地的距離是16千米,
設乙的速度是x千米/分鐘,由題意,得:
10x+16×![]() =16,
=16,
解得x=![]() 千米/分鐘,
千米/分鐘,
∴甲、乙相遇時,乙所行駛的路程:10×![]() =
=![]() (千米)
(千米)
(2)相遇后乙到達A站還需(16×![]() )÷
)÷![]() =2分鐘,
=2分鐘,
相遇后甲到達B站還需(10×![]() )÷
)÷![]() =80分鐘,
=80分鐘,
當乙到達終點A時,甲還需80﹣2=78分鐘到達終點B.


科目:初中數學 來源: 題型:
【題目】如圖所示平面內,有一靠在墻面上的梯子AB(粗細忽略不計),因外界因素導致梯子底端A持續向右滑動,直至整架梯子完全滑落到地面(即B與O重合),設A向右滑動的距離為x(cm),梯子的中點M與墻角O之間的距離為y(cm),則在整個滑動過程中,y與x的關系大致可表達為下列圖象中的( )
A.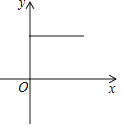
B.
C.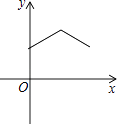
D.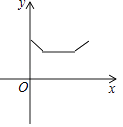
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】水龍頭關閉不緊會造成滴水,小明用可以顯示水量的容器做圖①所示的試驗,并根據試驗數據繪制出圖②所示的容器內盛水量W(L)與滴水時間t(h)的函數關系圖象,請結合圖象解答下列問題:
(1)容器內原有水多少?
(2)求W與t之間的函數關系式,并計算在這種滴水狀態下一天的滴水量是多少升?

圖 ① 圖②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分8分)
為了加強學生課外閱讀,開闊視野,某校開展了“書香校園,從我做起”的主題活動.學校隨機抽取了部分學生,對他們一周的課外閱讀時間進行調查,繪制出頻數分布表和頻數分布直方圖的一部分如下:


請根據圖表信息回答下列問題:
(1)頻數分布表中的![]() ,
,![]() ;
;
(2)將頻數分布直方圖補充完整;
(3)學校將每周課外閱讀時間在![]() 小時以上的學生評為“閱讀之星”,請你估計該校
小時以上的學生評為“閱讀之星”,請你估計該校![]() 名學生中評為“閱讀之星”的有多少人?
名學生中評為“閱讀之星”的有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司投資新建了一商場,共有商鋪30間.據預測,當每間的年租金定為10萬元時,可全部租出.每間的年租金每增加5000元,少租出商鋪1間.該公司要為租出的商鋪每間每年交各種費用1萬元,未租出的商鋪每間每年交各種費用5000元.
(1)當每間商鋪的年租金定為13萬元時,能租出多少間?
(2)當每間商鋪的年租金定為多少萬元時,該公司的年收益(收益=租金﹣各種費用)為275萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分別找一點M、N,使三角形AMN周長最小時,則∠AMN+∠ANM的度數為( )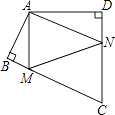
A.80°
B.90°
C.100°
D.130°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形OABC中,OA=3,OC=2,F是AB上的一個動點(F不與A,B重合),過點F的反比例函數y= ![]() (k>0)的圖象與BC邊交于點E.
(k>0)的圖象與BC邊交于點E.
(1)當F為AB的中點時,求該函數的解析式;
(2)當k為何值時,△EFA的面積為 ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中央電視臺舉辦的“中國詩詞大會”節目受到中學生的廣泛關注.某中學為了解該校九年級學生對觀看“中國詩詞大會”節目的喜愛程度,對該校九年級部分學生進行了隨機抽樣調查,并繪制出如圖所示的兩幅統計圖.在條形圖中,從左向右依次為:A 級(非常喜歡),B 級(較喜歡),C 級(一般),D 級(不喜歡).請結合兩幅統計圖,回答下列問題: 
(1)本次抽樣調查的樣本容量是 , 表示“D級(不喜歡)”的扇形的圓心角為°;
(2)若該校九年級有200名學生.請你估計該年級觀看“中國詩詞大會”節目B 級(較喜歡)的學生人數;
(3)若從本次調查中的A級(非常喜歡)的5名學生中,選出2名去參加廣州市中學生詩詞大會比賽,已知A級學生中男生有3名,請用“列表”或“畫樹狀圖”的方法求出所選出的2名學生中至少有1名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,M、N分別是正方形ABCD的邊BC、CD上的點,已知:∠MAN=30°,AM=AN,△AMN的面積為1. 
(1)求∠BAM的度數;
(2)求正方形ABCD的邊長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com