
【題目】如圖,已知一次函數(shù)![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,一次函數(shù)
,一次函數(shù)![]() 經(jīng)過點
經(jīng)過點![]() 與
與![]() 軸交于點.
軸交于點.
(1)求直線![]() 的解析式;
的解析式;
(2)點![]() 為
為![]() 軸上方直線
軸上方直線![]() 上一點,點
上一點,點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 為線段
為線段![]() 的中點,連接
的中點,連接![]() ,取
,取![]() 的中點
的中點![]() ,射線
,射線![]() 交
交![]() 軸于點
軸于點![]() ,點
,點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 為線段
為線段![]() 的中點,連接
的中點,連接![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,延長![]() 至
至![]() ,使
,使![]() ,連接
,連接![]() 、
、![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.
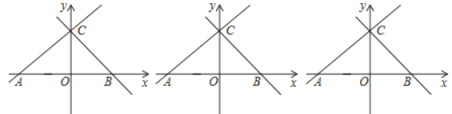
【答案】(1)![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)![]()
【解析】
(1)利用待定系數(shù)法即可解決問題;
(2)根據(jù)三角形的中位線定理即可證明;
(3)如圖2中,延長GF交AQ于K,連接PE.想辦法證明AE=EH=BH,可得H(1,0),再證明PA=PH,可得PE⊥AH,設(shè)AE=EH=x,構(gòu)建方程求出x即可解決問題.
(1)∵一次函數(shù)![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,
∴![]() ,
,![]() .
.
∵一次函數(shù)![]() 經(jīng)過點
經(jīng)過點![]() ,
,
∴![]() ,
,
∴一次函數(shù)的解析式為![]() .
.
(2)證明:如圖1中,連接![]() .
.
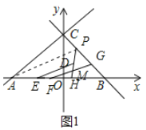
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
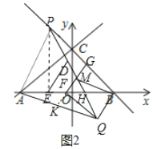
(3)如圖2中,延長![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴![]() ,設(shè)
,設(shè)![]() ,則
,則![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
設(shè)![]() ,
,
則![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】.Rt△ABC中,已知∠C=90°,∠B=50°,點D在邊BC上,BD=2CD(圖4).把△ABC繞著點D逆時針旋轉(zhuǎn)m(0<m<180)度后,如果點B恰好落在初始Rt△ABC的邊上,那么m=_________![]() .
.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】若一個三角形一條邊的平方等于另兩條的乘積,我們把這個三角形叫做比例三角形.
(1)已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,請直接寫出所有滿足條件的
,請直接寫出所有滿足條件的![]() 的長;
的長;
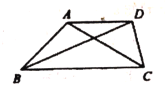
(2)如圖,在四邊形![]() 中,
中,![]() ,對角線
,對角線![]() 平分
平分![]() ,
,![]() .求證:
.求證:![]() 是比例三角形;
是比例三角形;
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
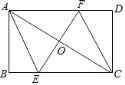
【題目】如圖,已知AC是矩形ABCD的對角線,AC的垂直平分線EF分別交BC、AD于點E和F,EF交AC于點O.
(1)求證:四邊形AECF是菱形;(2)若AB=6,AD=8,求四邊形AECF的周長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
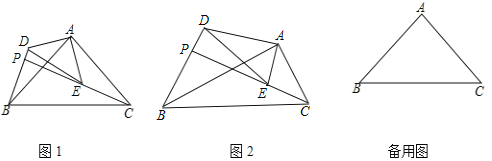
【題目】如圖,![]() 和
和![]() 是有公共頂點的直角三角形,
是有公共頂點的直角三角形,![]() ,點P為射線BD,CE的交點.
,點P為射線BD,CE的交點.
(1)如圖1,若![]() 和
和![]() 是等腰三角形,求證:
是等腰三角形,求證:![]() ;
;
(2)如圖2,若![]() ,問:(1)中的結(jié)論是否成立?請說明理由.
,問:(1)中的結(jié)論是否成立?請說明理由.
(3)在(1)的條件下,若![]() ,
,![]() ,若把
,若把![]() 繞點A旋轉(zhuǎn),當
繞點A旋轉(zhuǎn),當![]() 時,求PB的長.
時,求PB的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
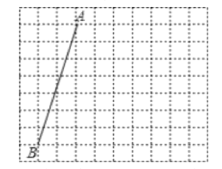
【題目】如圖,方格紙中每個小正方形的邊長均為1.線段AB的兩個端點在小正方形的頂點上。
(1)在圖中畫一個以AB為腰的等腰三角形△ABC點C在小正方形的頂點上,且tan∠B=3;
(2)在圖中畫一個以AB為底的等腰三角形△ABD點D在小正方形的項點上,且△ABD是銳角三角形。連接CD,請直接寫出線段CD的長。
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】小賢放學回家看到桌上有4塊糖果,其中有玉米味、奶油味的糖果各1塊,椰子味的糖果2塊,這些糖果除味道外無其他差別.
(1)小賢隨機地從盤中取出一塊糖果,取出的是玉米味糖果的概率是多少?
(2)小賢隨機地從盤中取出兩塊糖果,試用畫樹狀圖或列表的方法表示所有可能的結(jié)果,并求出小賢取出的兩個都是椰子味糖果的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com