
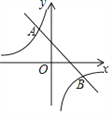
【題目】如圖,一次函數y=k1x+b與反比例函數y=![]() 的圖象交于點A(m,2),B(2,-1).
的圖象交于點A(m,2),B(2,-1).
(1)求這兩個函數的表達式;
(2)在x軸上是否存在點P(n,0),使△ABP為直角三角形,請你直接寫出P點的坐標.
【答案】(1)![]() ;y=-x+1;(2)P點的坐標(3,0)、(﹣3,0)、(
;y=-x+1;(2)P點的坐標(3,0)、(﹣3,0)、(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】分析:(1)把點B坐標代入y=![]() 求出反比例函數的解析式,再把點A坐標代入反比例函數的解析式求出m的值,利用待定系數法求出一次函數解析式.
求出反比例函數的解析式,再把點A坐標代入反比例函數的解析式求出m的值,利用待定系數法求出一次函數解析式.
(2)分三種情況進行討論, ①當∠BAP=90°; ②當∠BPA=90°; ③當∠PBA=90°, 利用勾股定理的逆定理建立方程即可得出結論.
詳解: (1)把A(1,2)代入y=![]() 得:2=k 1
得:2=k 1
∴k =2×(1)=2
∴![]()
把B(m,2)代入![]() 得:m=-1,
得:m=-1,
∴B(-1,2)
把A(1,2),B(2,1)分別代入y=k x+b得:
![]()
∴![]()
∴y=x+1
(2)∵A(1,2),B(2,1),P(n,0),
∴AB =18,AP =(n+1) +4,BP =(n2) +1,
∵△ABP為直角三角形,
∴①當∠ABP=90°時,AB +BP =AP ,
∴18+(n2) +1=(n+1) +4,
∴n=3,
∴P(3,0),
②當∠BAP=90°時,AB +AP =BP ,
∴18+(n+1) +4=(n2) +1,
∴n=3,
∴P(3,0),
③當∠APB=90°時,AP +BP =AB ,
∴(n+1) +4+(n2) +1=18,
∴n=![]() ,
,
∴P(![]() ,0)或(
,0)或(![]() ,0)
,0)
即:P點的坐標(3,0)、(3,0)、(![]() ,0)或(
,0)或(![]() ,0).
,0).
點睛: 本題考查反比例函數和一次函數解析式的確定、等腰直角三角形的判定等知識及綜合應用知識、解決問題的能力.要注意在不確定直角三角形的直角邊和底邊的情況下要考慮到所有的情況,不要漏解.


科目:初中數學 來源: 題型:
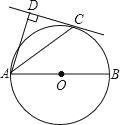
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,AD和過C點的切線互相垂直,垂足為D.
(1)求證:AC平分∠DAB;
(2)過點O作線段AC的垂線OE,垂足為E(要求:尺規作圖,保留作圖痕跡,不寫作法);
(3)若CD=4,AC=4![]() ,求垂線段OE的長.
,求垂線段OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
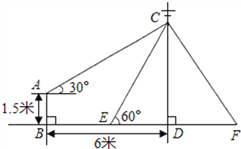
【題目】如圖,在電線桿上的C處引拉線CE、CF固定電線桿,拉線CE和地面所成的角
∠CED=60°,在離電線桿6米的B處安置測角儀AB,在A處測得電線桿上C處的仰角為30°,已知測角儀高AB為1.5米,求拉線CE的長 (結果精確到0.1米,參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中數學 來源: 題型:
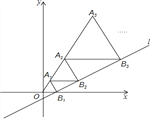
【題目】如圖,在平面直角坐標系中,直線l:y=![]() x﹣
x﹣![]() 與x軸交于點B1,以OB1為邊長作等邊三角形A1OB1,過點A1作A1B2平行于x軸,交直線l于點B2,以A1B2為邊長作等邊三角形A2A1B2,過點A2作A2B3平行于x軸,交直線l于點B3,以A2B3為邊長作等邊三角形A3A2B3,…,則點A100的橫坐標是_____.
與x軸交于點B1,以OB1為邊長作等邊三角形A1OB1,過點A1作A1B2平行于x軸,交直線l于點B2,以A1B2為邊長作等邊三角形A2A1B2,過點A2作A2B3平行于x軸,交直線l于點B3,以A2B3為邊長作等邊三角形A3A2B3,…,則點A100的橫坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
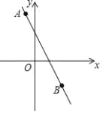
【題目】在直角坐標系中,一條直線經過A(﹣1,5),P(2,a),B(3,﹣3).
(1)求直線AB的函數表達式;
(2)求a的值;
(3)求△AOP的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,貨輪O在航行過程中,發現燈塔A在它北偏東30°的方向上,海島B在它南偏東60°方向上.則下列結論:
①∠NOA=30°;
②圖中∠NOB的補角有兩個,分別是∠SOB和∠EOA;
③圖中有4對互余的角;
④貨輪O在海島B的西偏北30°的方向上.
其中正確結論的個數有( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
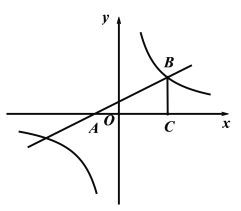
【題目】已知:如圖,在平面直角坐標系xOy中,直線![]() 與x軸交于點A,在第一象限內與反比例函數圖像交于點B,BC垂直于x軸,垂足為點C,且OC=2AO.求
與x軸交于點A,在第一象限內與反比例函數圖像交于點B,BC垂直于x軸,垂足為點C,且OC=2AO.求
(1)點![]() 的坐標;
的坐標;
(2)反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,□ABCD中,AB=2,BC=![]() .
.
(1)利用尺規作∠ABC的平分線BE,交AD于點E;(保留作圖痕跡,不寫作法)
(2)記![]() ,先化簡
,先化簡![]() ,再求
,再求![]() 的值.
的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com