
【題目】如圖1,在![]() 中,
中,![]() 于點(diǎn)
于點(diǎn)![]() 的垂直平分線交
的垂直平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,
,![]() .
.
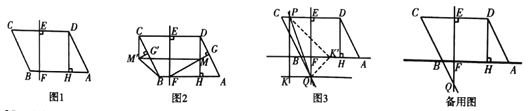
(1)如圖2,作![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,將
,將![]() 沿
沿![]() 方向平移,得到
方向平移,得到![]() ,連接
,連接![]() .
.
①求四邊形![]() 的面積;
的面積;
②直線![]() 上有一動點(diǎn)
上有一動點(diǎn)![]() ,求
,求![]() 周長的最小值.
周長的最小值.
(2)如圖3.延長![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() .過點(diǎn)
.過點(diǎn)![]() 作
作![]() ,過
,過![]() 邊上的動點(diǎn)
邊上的動點(diǎn)![]() 作
作![]() ,并與
,并與![]() 交于點(diǎn)
交于點(diǎn)![]() ,將
,將![]() 沿直線
沿直線![]() 翻折,使點(diǎn)
翻折,使點(diǎn)![]() 的對應(yīng)點(diǎn)
的對應(yīng)點(diǎn)![]() 恰好落在直線
恰好落在直線![]() 上,求線段
上,求線段![]() 的長.
的長.
【答案】(1)①![]() ;②
;②![]() 周長的最小值為9;(2)
周長的最小值為9;(2)![]() 的長為
的長為![]() 或
或![]() .
.
【解析】(1)①根據(jù)相似三角形的判定和性質(zhì)以及平移的性質(zhì)進(jìn)行解答即可;
②連接CM交直線EF于點(diǎn)N,連接DN,利用勾股定理解答即可;
(2)分點(diǎn)P在線段CE上和點(diǎn)P在線段ED上兩種情況進(jìn)行解答.
(1)①在ABCD中,AB=6,直線EF垂直平分CD,
∴DE=FH=3,
又BF:FA=1:5,
∴AH=2,
∵Rt△AHD∽Rt△MHF,
∴![]() ,即
,即![]() ,
,
∴HM=1.5,
根據(jù)平移的性質(zhì),MM'=CD=6,連接BM,如圖1,
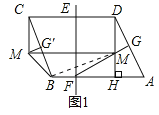
四邊形BHMM′的面積=![]() ×6×1.5+
×6×1.5+![]() ×4×1.5=7.5;
×4×1.5=7.5;
②連接CM交直線EF于點(diǎn)N,連接DN,如圖2,
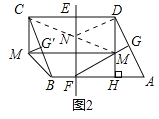
∵直線EF垂直平分CD,
∴CN=DN,
∵MH=1.5,
∴DM=2.5,
在Rt△CDM中,MC2=DC2+DM2,
∴MC2=62+(2.5)2,
即MC=6.5,
∵MN+DN=MN+CN=MC,
∴△DNM周長的最小值為9.
(2)∵BF∥CE,
∴![]() ,
,
∴QF=2,
∴PK=PK'=6,
過點(diǎn)K'作E'F'∥EF,分別交CD于點(diǎn)E',交QK于點(diǎn)F',如圖3,
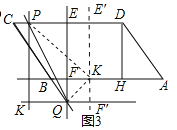
當(dāng)點(diǎn)P在線段CE上時(shí),
在Rt△PK'E'中,
PE'2=PK'2-E'K'2,
∴PE′=2![]() ,
,
∵Rt△PE'K'∽Rt△K'F'Q,
∴![]() ,即
,即![]() ,
,
解得:QF′=![]() ,
,
∴PE=PE'-EE'=2![]()
![]() =
=![]() ,
,
∴CP=![]() ,
,
同理可得,當(dāng)點(diǎn)P在線段DE上時(shí),CP′=![]() ,如圖4,
,如圖4,
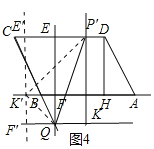
綜上所述,CP的長為![]() 或
或![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知多項(xiàng)式![]()
(1)若多項(xiàng)式的值與字母![]() 的取值無關(guān),求
的取值無關(guān),求![]() ,
,![]() 的值;
的值;
(2)在(1)的條件下,先化簡多項(xiàng)式![]() ,再求它的值;
,再求它的值;
(3)在(1)的條件下,求![]() 的值
的值
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)已知A.B是直線上的兩點(diǎn),且AB=6,若P在這條直線上,且PA=5.
①畫出P點(diǎn)在直線AB上的大致位置圖;
②求PB長.
(2)尺規(guī)作圖(不寫作法.保留作圖痕跡)
已知線段![]() ,求作:線段MN,使MN=
,求作:線段MN,使MN=![]() .
.
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】探究:如圖①, ![]() ,試說明
,試說明![]() .下面給出了這道題的解題過程,請?jiān)谙铝薪獯鹬校钌线m當(dāng)?shù)睦碛桑?/span>
.下面給出了這道題的解題過程,請?jiān)谙铝薪獯鹬校钌线m當(dāng)?shù)睦碛桑?/span>
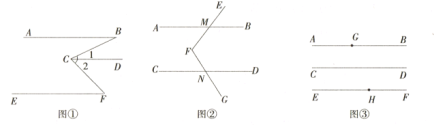
解: ∵![]() .(已知)
.(已知)
∴ ![]() .( )
.( )
同理可證, ![]() .
.
∵ ![]() ,
,
∴![]() .( )
.( )
應(yīng)用:如圖②, ![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 之間,
之間,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() .若
.若![]() ,
,![]() ,則
,則![]() 的大小為_____________度.
的大小為_____________度.
拓展:如圖③,直線![]() 在直線
在直線![]() 之間,且
之間,且![]() ,點(diǎn)
,點(diǎn)![]() 分別在直線
分別在直線![]() 上,點(diǎn)
上,點(diǎn)![]() 是直線
是直線![]() 上的一個動點(diǎn),且不在直線
上的一個動點(diǎn),且不在直線![]() 上,連結(jié)
上,連結(jié)![]() .若
.若![]() ,則
,則![]() =________度.
=________度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,BD為△ABC外接圓⊙O的直徑,且∠BAE=∠C.
(1)求證:AE與⊙O相切于點(diǎn)A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的長.
,求AD的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某項(xiàng)工程由甲乙兩隊(duì)分別單獨(dú)完成,則甲隊(duì)用時(shí)是乙隊(duì)的1.5倍:若甲乙兩隊(duì)合作,則需12天完成,請問:
(1)甲,乙兩隊(duì)單獨(dú)完成各需多少天;
(2)若施工方案是甲隊(duì)先單獨(dú)施工![]() 天,剩下工程甲乙兩隊(duì)合作完成,若甲隊(duì)施工費(fèi)用為每天1.5萬元,乙隊(duì)施工費(fèi)為每天3.5萬元求施工總費(fèi)用
天,剩下工程甲乙兩隊(duì)合作完成,若甲隊(duì)施工費(fèi)用為每天1.5萬元,乙隊(duì)施工費(fèi)為每天3.5萬元求施工總費(fèi)用![]() (萬元)關(guān)于施工時(shí)間
(萬元)關(guān)于施工時(shí)間![]() (天)的函數(shù)關(guān)系式
(天)的函數(shù)關(guān)系式
(3)在(2)的方案下,若施工期定為15~18天內(nèi)完成(含15和18天),如何安排施工方案使費(fèi)用最少,最少費(fèi)用為多少萬元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】初三年級學(xué)習(xí)壓力大,放學(xué)后在家自學(xué)時(shí)間較初一、初二長,為了解學(xué)生學(xué)習(xí)時(shí)間,該年級隨機(jī)抽取25%的學(xué)生問卷調(diào)查,制成統(tǒng)計(jì)表和扇形統(tǒng)計(jì)圖,請你根據(jù)圖表中提供的信息回答下列問題:
學(xué)習(xí)時(shí)間(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人數(shù) | 72 | 36 | 54 | 18 |
(1)初三年級共有學(xué)生_____人.
(2)在表格中的空格處填上相應(yīng)的數(shù)字.
(3)表格中所提供的學(xué)生學(xué)習(xí)時(shí)間的中位數(shù)是_____,眾數(shù)是_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方形ABCD中,點(diǎn)E,F(xiàn)分別在邊BC,CD上,且BE=CF.連接AE,BF,AE與BF交于點(diǎn)G.下列結(jié)論錯誤的是( )
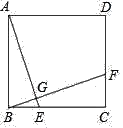
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
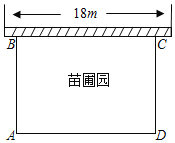
【題目】某中學(xué)課外興趣活動小組準(zhǔn)備圍建一個矩形的苗圃圓.其中一邊靠墻,另外三邊用長為40m的籬笆圍成.已知墻長為18m(如圖所示),設(shè)這個苗圃園垂直于墻的一邊AB為xm
(1)用含有x的式子表示AD,并寫出x的取值范圍;
(2)若苗圃園的面積為192m2平方米,求AB的長度.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com