
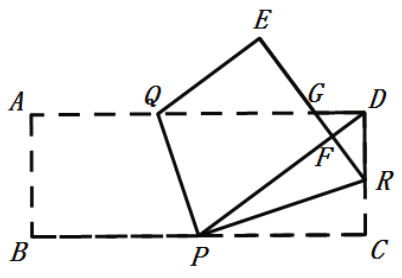
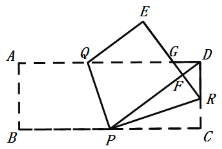
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() .點
.點![]() 在
在![]() 上,連接
上,連接![]() ,折疊矩形,點
,折疊矩形,點![]() 與點
與點![]() 都恰好落在
都恰好落在![]() 上的點
上的點![]() 處,折痕是
處,折痕是![]() 、
、![]() 、
、![]() 的對應線段
的對應線段![]() 與
與![]() 交于點
交于點![]() ,則線段
,則線段![]() 的長度是______.
的長度是______.
【答案】![]() ;
;
【解析】
根據折疊的性得到PC=PF =4,FR=RC,在Rt△PDC中,求得PD、DF的長,在Rt△DFR中,求得![]() ,證得Rt△DFR
,證得Rt△DFR![]() Rt△GFD,求得
Rt△GFD,求得![]() ,再證得Rt△EGQ
,再證得Rt△EGQ![]() Rt△FGD,即可求解.
Rt△FGD,即可求解.
∵折疊矩形,點![]() 與點
與點![]() 都恰好落在
都恰好落在![]() 上的點
上的點![]() 處,
處,
∴PC=PF=PB,
∵矩形![]() 中,
中,![]() ,
,![]() ,
,
∴BC=AD=8,AB=CD=3,
∴PC=PF=![]() BC=4,
BC=4,
在Rt△PDC中,PD=![]() ,
,
∴DF=PD-PF=5-4=1,
根據折疊的性質,△PCR![]() △PFR,
△PFR,
∴RC=FR,∠C=∠PFR=90![]() ,
,
在Rt△DFR中,DF=1,DR=CD-RC=3-FR,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
在Rt△FDR和Rt△FGD中,
∠FDR+∠FDG=90![]() ,∠FGD+∠FDG=90
,∠FGD+∠FDG=90![]() ,
,
∴∠FDR=∠FGD,
∴Rt△DFR![]() Rt△GFD,
Rt△GFD,
∴![]() ,即
,即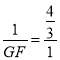 ,
,
∴![]() ,
,
∴DG=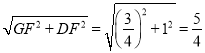 ,
,
根據折疊的性質,EF=AB=3,∠E=∠B=90![]() ,
,
∴EG=EF-GF=3-![]() ,
,
∵∠E=∠DFG=90![]() ,∠EGQ=∠FGD,
,∠EGQ=∠FGD,
∴Rt△EGQ![]() Rt△FGD,
Rt△FGD,
∴![]() ,即
,即 ,
,
∴QG=![]() (
(![]() ) .
) .
故答案為:![]() .
.


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx-3(a≠0)經過點(-2,-3).
(1)用a表示b.
(2)當x≥-2時,y≤-2,求拋物線的解析式.
(3)無論a取何值,若一次函數y2=a2x+m總經過y的頂點,求證:m≥![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知二次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,![]() ,對稱軸為直線
,對稱軸為直線![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是關于
是關于![]() 的一元二次方程
的一元二次方程![]() 的一個根.其中正確的有( )
的一個根.其中正確的有( )
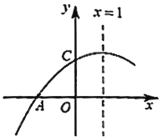
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:如果關于x的一元二次方程ax2+bx+c=0(a≠0)有兩個實數根,且其中一個根是另一個根的2倍,則稱這樣的方程為“倍根方程”.現有下列結論: ①方程x2+2x﹣8=0是倍根方程;
②若關于x的方程x2+ax+2=0是倍根方程,則a=±3;
③若關于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,則拋物線y=ax2﹣6ax+c與x軸的公共點的坐標是(2,0)和(4,0);
④若點(m,n)在反比例函數y=![]() 的圖象上,則關于x的方程mx2+5x+n=0是倍根方程.
的圖象上,則關于x的方程mx2+5x+n=0是倍根方程.
上述結論中正確的有( )
A. ①② B. ③④ C. ②③ D. ②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】扶貧工作小組對果農進行精準扶貧,幫助果農將一種有機生態水果拓寬了市場.與去年相比,今年這種水果的產量增加了1000千克,每千克的平均批發價比去年降低了1元,批發銷售總額比去年增加了![]() .
.
(1)已知去年這種水果批發銷售總額為10萬元,求這種水果今年每千克的平均批發價是多少元?
(2)某水果店從果農處直接批發,專營這種水果.調查發現,若每千克的平均銷售價為41元,則每天可售出300千克;若每千克的平均銷售價每降低3元,每天可多賣出180千克,設水果店一天的利潤為![]() 元,當每千克的平均銷售價為多少元時,該水果店一天的利潤最大,最大利潤是多少?(利潤計算時,其它費用忽略不計.)
元,當每千克的平均銷售價為多少元時,該水果店一天的利潤最大,最大利潤是多少?(利潤計算時,其它費用忽略不計.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形![]() 是正方形,點
是正方形,點![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的點,且
上的點,且![]() ,連接
,連接![]() 、
、![]() 交于點
交于點![]() .
.
(1)如圖①,判斷![]() 和
和![]() 之間的數量關系和位置關系,并證明;
之間的數量關系和位置關系,并證明;
(2)如圖②,連接![]() ,點
,點![]() 是
是![]() 中點,若
中點,若![]() ,
,![]() ,求線段
,求線段![]() 的長度;
的長度;
(3)如圖③,作![]() 于點
于點![]() ,若
,若![]() ,求證:點
,求證:點![]() 是
是![]() 中點.
中點.
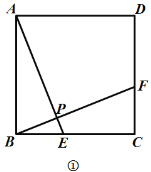
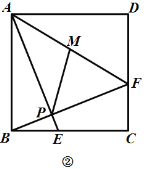
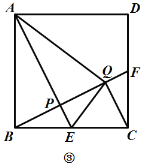
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明從家去上學,先步行一段路,因時間緊,他改騎共享單車,結果到學校時遲到了7min,其行駛的路程![]() (單位:
(單位:![]() )與時間
)與時間![]() (單位:
(單位:![]() )的關系如圖.若他出門時直接騎共享單車(兩次騎車速度相同),則下列說法正確的是( )
)的關系如圖.若他出門時直接騎共享單車(兩次騎車速度相同),則下列說法正確的是( )
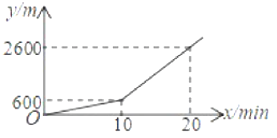
A.小明會遲到2min到校B.小明剛好按時到校
C.小明可以提前1min到校D.小明可以提前2min到校
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人在環形跑道上同起點、同終點、同方向勻速跑步400米,先到終點的人原地休息.已知甲先出發2秒.在跑步過程中,甲、乙兩人的距離![]() (單位:
(單位:![]() )與乙出發的時間
)與乙出發的時間![]() (單位:
(單位:![]() )之間的關系如圖所示,下列說法:①甲的速度為
)之間的關系如圖所示,下列說法:①甲的速度為![]() ;②乙的速度為
;②乙的速度為![]() ;③乙出發
;③乙出發![]() 時甲、乙兩人之間的距離為
時甲、乙兩人之間的距離為![]() ;④甲到達終點時乙在終點休息了
;④甲到達終點時乙在終點休息了![]() ;⑤
;⑤![]() ,其中的正確的個數有( )
,其中的正確的個數有( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 位于點
位于點![]() 的左側),與
的左側),與![]() 軸的負半軸交于點
軸的負半軸交于點![]() .
.
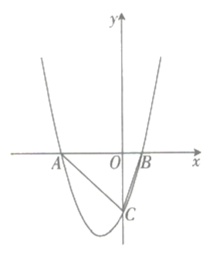
![]() 求點
求點![]() 的坐標.
的坐標.
![]() 若
若![]() 的面積為
的面積為![]() .
.
①求這條拋物線相應的函數解析式.
②在拋物線上是否存在一點![]() 使得
使得![]() ?若存在,請求出點
?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com