
【題目】如圖1,![]() 中,
中,![]() ,將扇形
,將扇形![]() 按圖1擺放,使扇形的半徑
按圖1擺放,使扇形的半徑![]() 、
、![]() 分別與
分別與![]() 、
、![]() 重合,
重合,![]() .
.
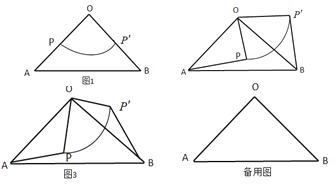
如圖2,若![]() 不動(dòng),讓扇形
不動(dòng),讓扇形![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)一周,連接線段
逆時(shí)針旋轉(zhuǎn)一周,連接線段![]() 、
、![]() ,設(shè)旋轉(zhuǎn)角為
,設(shè)旋轉(zhuǎn)角為![]() .
.
發(fā)現(xiàn):直接寫出![]() 、
、![]() 的數(shù)量關(guān)系.
的數(shù)量關(guān)系.
探究:若![]()
(1)扇形![]() 繞到點(diǎn)
繞到點(diǎn)![]() 的左側(cè),當(dāng)
的左側(cè),當(dāng)![]() 時(shí),旋轉(zhuǎn)角
時(shí),旋轉(zhuǎn)角![]() ______°;
______°;
(2)扇形![]() 繞到點(diǎn)
繞到點(diǎn)![]() 的右側(cè),當(dāng)
的右側(cè),當(dāng)![]() 與
與![]() 相切時(shí),求
相切時(shí),求![]() ;
;
(3)若點(diǎn)![]() 是弧
是弧![]() 上任意一點(diǎn),在扇形
上任意一點(diǎn),在扇形![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針轉(zhuǎn)過程中,當(dāng)
逆時(shí)針轉(zhuǎn)過程中,當(dāng)![]() 的面積最大時(shí),直接寫出
的面積最大時(shí),直接寫出![]() 的度數(shù);
的度數(shù);
延伸:如圖3,若![]() ,當(dāng)
,當(dāng)![]() 、
、![]() 、
、![]() 三點(diǎn)共線時(shí),直接寫出線段
三點(diǎn)共線時(shí),直接寫出線段![]() 的長(zhǎng).
的長(zhǎng).
【答案】發(fā)現(xiàn)![]() ;探究:(1)310;(2)
;探究:(1)310;(2)![]() ;(3)
;(3)![]() 或
或![]() ;延伸:
;延伸:![]() 或
或![]() .
.
【解析】
發(fā)現(xiàn):根據(jù)OA=OB,OP=O![]() 即可得到
即可得到![]() ;
;
探究:(1)根據(jù)題意畫出圖形,由OP∥AB得到∠AOP=∠A=50°,即可求出旋轉(zhuǎn)角![]()
![]() ;
;
(2)由![]() 與
與![]() 相切得到
相切得到![]() 是直角三角形,根據(jù)勾股定理求出AP即可得到B
是直角三角形,根據(jù)勾股定理求出AP即可得到B![]() ;
;
(3)根據(jù)![]() 的面積=OQ乘以過點(diǎn)A作OQ的高線的積的一半,故當(dāng)高線恰好是OA時(shí),
的面積=OQ乘以過點(diǎn)A作OQ的高線的積的一半,故當(dāng)高線恰好是OA時(shí),![]() 的面積最大,由此得到
的面積最大,由此得到![]() 的度數(shù);
的度數(shù);
延伸:根據(jù)題意畫出圖形,利用等腰三角形的三線合一的性質(zhì)及三角函數(shù)求出OH,利用勾股定理求出AH,即可得到答案.
發(fā)現(xiàn):∵OA=OB,OP=O![]() ,
,
∴OA-OP=OB-O![]() ,
,
即![]() ;
;
探究:
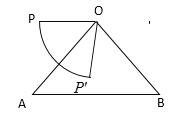
(1)如圖:
∵![]() ,OA=OB,
,OA=OB,
∴∠A=∠B=50°,
∵OP∥AB,
∴∠AOP=∠A=50°,
∴旋轉(zhuǎn)角![]()
![]() ,
,
故答案為:310;
(2)解:∵![]() 與
與![]() 相切,
相切,
∴![]() 即
即![]() 是直角三角形,
是直角三角形,
∴![]() ,
,
∴![]() ;
;
(3)∵點(diǎn)Q在![]() 上,
上,
∴OQ=OP,
![]() 的面積=OQ乘以過點(diǎn)A作OQ的高線的積的一半,故當(dāng)高線恰好是OA時(shí),
的面積=OQ乘以過點(diǎn)A作OQ的高線的積的一半,故當(dāng)高線恰好是OA時(shí),![]() 的面積最大,
的面積最大,
∴![]() =90°-80°=10°或
=90°-80°=10°或![]() =180°-10°=170°;
=180°-10°=170°;
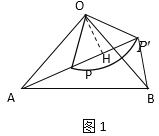
延伸:過點(diǎn)O作OH⊥P![]() 于H,如圖1,
于H,如圖1,
∵∠PO![]() =90°,OP=O
=90°,OP=O![]() =6,
=6,
∴OH=PH=![]() ,
,
∵OA=10,
∴AH=![]() ,
,
∴B![]() =AP=
=AP=![]() ;
;
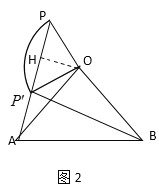
過點(diǎn)O作OH⊥P![]() 于H,如圖2,
于H,如圖2,
∵∠PO![]() =90°,OP=O
=90°,OP=O![]() =6,
=6,
∴OH=PH=![]() ,
,
∵OA=10,
∴AH=![]() ,
,
∴B![]() =AP=
=AP=![]() ;
;
∴線段![]() 的長(zhǎng)為
的長(zhǎng)為![]() 或
或![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
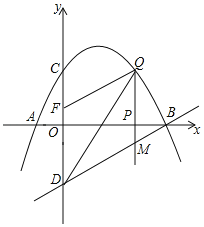
【題目】如圖,已知拋物線y=﹣![]() +bx+c的圖象經(jīng)過點(diǎn)A(﹣1,0)和點(diǎn)C(0,2),點(diǎn)D與點(diǎn)C關(guān)于x軸對(duì)稱,點(diǎn)P是x軸上的一個(gè)動(dòng)點(diǎn),設(shè)點(diǎn)P的坐標(biāo)為(m,0),過點(diǎn)P作x軸的垂線l交拋物線于點(diǎn)Q,交直線BD于點(diǎn)M.
+bx+c的圖象經(jīng)過點(diǎn)A(﹣1,0)和點(diǎn)C(0,2),點(diǎn)D與點(diǎn)C關(guān)于x軸對(duì)稱,點(diǎn)P是x軸上的一個(gè)動(dòng)點(diǎn),設(shè)點(diǎn)P的坐標(biāo)為(m,0),過點(diǎn)P作x軸的垂線l交拋物線于點(diǎn)Q,交直線BD于點(diǎn)M.
(1)求該拋物線所表示的二次函數(shù)的表達(dá)式.
(2)已知點(diǎn)F(0,![]() ),當(dāng)點(diǎn)P在x軸正半軸上運(yùn)動(dòng)時(shí),試求m為何值時(shí),四邊形DMQF是平行四邊形?
),當(dāng)點(diǎn)P在x軸正半軸上運(yùn)動(dòng)時(shí),試求m為何值時(shí),四邊形DMQF是平行四邊形?
(3)點(diǎn)P在線段AB運(yùn)動(dòng)過程中,是否存在點(diǎn)Q,使得以點(diǎn)B、Q、M為頂點(diǎn)的三角形與△BOD相似?若存在,求出點(diǎn)Q的坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
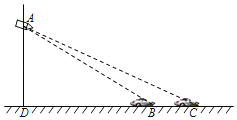
【題目】如圖,一輛轎車在經(jīng)過某路口的感應(yīng)線B和C處時(shí),懸臂燈桿上的電子警察拍攝到兩張照片,兩感應(yīng)線之間距離BC為6m,在感應(yīng)線B、C兩處測(cè)得電子警察A的仰角分別為∠ABD=18°,∠ACD=14°.求電子警察安裝在懸臂燈桿上的高度AD的長(zhǎng).
(參考數(shù)據(jù):sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某班老師要求每人每學(xué)期讀4~7本書,并隨機(jī)抽查了本學(xué)期學(xué)生讀課外書冊(cè)數(shù)的情況,繪制成不完整的條形圖和不完整的扇形圖,其中條形圖被墨跡遮蓋了一部分,回答下列問題:
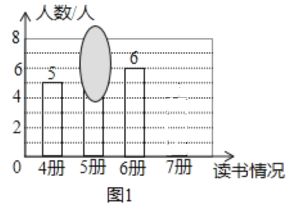

(1)請(qǐng)你求出老師隨機(jī)抽查了多少名學(xué)生;
(2)已知冊(cè)數(shù)的中位數(shù)是5,
嘉嘉說:條形圖中被遮蓋的數(shù)為5
淇淇說:條形圖中被遮蓋的數(shù)為6
ⅰ你認(rèn)為嘉嘉和淇淇誰說的正確,請(qǐng)說明原因,并把條形圖補(bǔ)充完整;
ⅱ在扇形圖中,“7冊(cè)”部分所對(duì)的圓心角為_______°,并把扇形圖補(bǔ)充完整;
(3)請(qǐng)直接寫出:從抽查學(xué)生中任取兩人,恰好都讀7冊(cè)書的概率為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
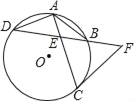
【題目】如圖所示,⊙O中,弦AC、BD交于E,![]() .
.
(1)求證:![]() ;
;
(2)延長(zhǎng)EB到F,使EF=CF,試判斷CF與⊙O的位置關(guān)系,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
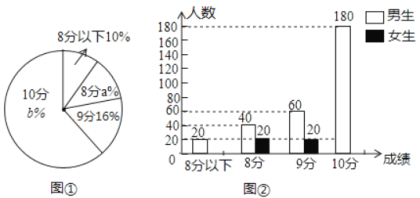
【題目】某中學(xué)對(duì)本校2018屆500名學(xué)生的中考體育測(cè)試情況進(jìn)行調(diào)查,根據(jù)男生1000米及女生800米測(cè)試成績(jī)整理,繪制成不完整的統(tǒng)計(jì)圖(圖①,圖②),請(qǐng)根據(jù)統(tǒng)計(jì)圖提供的信息,解答下列問題:
(1)該校畢業(yè)生中男生有 人;扇形統(tǒng)計(jì)圖中![]() ;500名學(xué)生中中考體育測(cè)試成績(jī)的中位數(shù)是 ;
;500名學(xué)生中中考體育測(cè)試成績(jī)的中位數(shù)是 ;
(2)補(bǔ)全條形統(tǒng)計(jì)圖;
(3)從500名學(xué)生中隨機(jī)抽取一名學(xué)生,這名學(xué)生該項(xiàng)成績(jī)?cè)?/span>8分及8分以下的概率是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,點(diǎn)O在斜邊AB上,以O(shè)為圓心,OB為半徑作圓,分別與BC,AB相交于點(diǎn)D,E,連結(jié)AD.已知∠CAD=∠B,
(1)求證:AD是⊙O的切線.
(2)若BC=8,tanB=![]() ,求⊙O 的半徑.
,求⊙O 的半徑.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
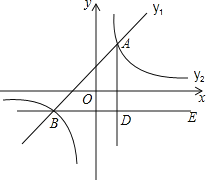
【題目】如圖,在平面直角坐標(biāo)系中,一次函數(shù)![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() 的圖象交于點(diǎn)
的圖象交于點(diǎn)![]() 和
和![]() .
.
![]() 求一次函數(shù)和反比例函數(shù)的表達(dá)式;
求一次函數(shù)和反比例函數(shù)的表達(dá)式;
![]() 請(qǐng)直接寫出
請(qǐng)直接寫出![]() 時(shí),x的取值范圍;
時(shí),x的取值范圍;
![]() 過點(diǎn)B作
過點(diǎn)B作![]() 軸,
軸,![]() 于點(diǎn)D,點(diǎn)C是直線BE上一點(diǎn),若
于點(diǎn)D,點(diǎn)C是直線BE上一點(diǎn),若![]() ,求點(diǎn)C的坐標(biāo).
,求點(diǎn)C的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com