
【題目】如圖,拋物線y=-![]() x2-
x2-![]() x+
x+![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸于點C,已知點D(0,-
與x軸交于A、B兩點(點A在點B的左側),與y軸于點C,已知點D(0,-![]() ).
).
(1)求直線AC的解析式;
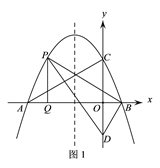
(2)如圖1,P為直線AC上方拋物線上的一動點,當△PBD的面積最大時,過P作PQ⊥x軸于點Q,M為拋物線對稱軸上的一動點,過M作y軸的垂線,垂足為點N,連接PM、NQ,求PM+MN+NQ的最小值;
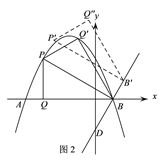
(3)在(2)問的條件下,將得到的△PBQ沿PB翻折得到△PBQ′,將△PBQ′沿直線BD平移,記平移中的△PBQ′為△P′B′Q″,在平移過程中,設直線P′B′與x軸交于點E,則是否存在這樣的點E,使得△B′EQ″為等腰三角形?若存在,求此時OE的長.
【答案】(1)直線AC的表達式為![]() ;(2)
;(2)![]() 的最小值為
的最小值為![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】分析:(1)求出![]() 兩點坐標,利用待定系數法即可解決問題;
兩點坐標,利用待定系數法即可解決問題;
![]() 過點P作y軸的平行線交直線BD于點F, 設點
過點P作y軸的平行線交直線BD于點F, 設點![]()
![]() ,則
,則![]() ,表示出
,表示出![]() 的長度,根據
的長度,根據![]() ,構建出二次函數,根據二次函數的性質求出最值即可.
,構建出二次函數,根據二次函數的性質求出最值即可.
![]() 分三種情況進行討論即可.
分三種情況進行討論即可.
詳解:(1)![]()
![]() 、
、![]() 、
、![]()
設直線AC的表達式為![]() ,將
,將![]() 、
、![]() 代入解析式:
代入解析式:
 可得
可得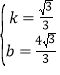 則直線AC的表達式為
則直線AC的表達式為![]() ;
;
(2)可得直線BD的解析式為![]() ,過點P作y軸的平行線交直線BD于點F,
,過點P作y軸的平行線交直線BD于點F,
設點![]()
![]() ,則
,則![]() .
.
![]() ,
,
![]() .
.
![]() 當
當![]() ,即
,即![]() 時,
時,![]() 最大;
最大;
則![]() ,過點P作對稱軸
,過點P作對稱軸![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,可得
,可得![]()
作![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,連接
,連接![]() ,交
,交![]() 軸與點
軸與點![]() ,
,
再過點![]() 作對稱軸
作對稱軸![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,即
,即![]() 、
、![]() 為所求點.
為所求點.
此時![]()
![]() ,則最小值為
,則最小值為![]() ;
;
(3)當![]() 時,
時,![]() 或
或![]()
當![]() 時,
時,![]() .
.
當![]() 時,
時,![]() .
.


科目:初中數學 來源: 題型:
【題目】“校園手機”現象越來越受到社會的關注.“寒假”期間,某校小記者隨機調查了某地區若干名學生和家長對中學生帶手機現象的看法,統計整理并制作了如下的統計圖:

(1)求這次調查的家長人數,并補全圖1;
(2)求圖2中表示家長“贊成”的圓心角的度數;
(3)已知某地區共6500名家長,估計其中反對中學生帶手機的大約有多少名家長?
查看答案和解析>>
科目:初中數學 來源: 題型:
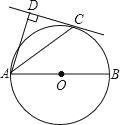
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,AD和過C點的切線互相垂直,垂足為D.
(1)求證:AC平分∠DAB;
(2)過點O作線段AC的垂線OE,垂足為E(要求:尺規作圖,保留作圖痕跡,不寫作法);
(3)若CD=4,AC=4![]() ,求垂線段OE的長.
,求垂線段OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機小張某天上午營運全是在東西走向的政府大道上進行的,如果規定向東為正,向西為負,他這天上午的行程是(單位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)將最后一名乘客送達目的地時,小張距上午出發點的距離是多少千米?在出發點的什么方向?
(2)若汽車耗油量為0.6升/千米,出車時,郵箱有油72.2升,若小張將最后一名乘客送達目的地,再返回出發地,問小張今天上午是否需要加油?若要加油至少需要加多少才能返回出發地?若不用加油,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一種密碼,將英文26個字舟a,b,c,…,z(不論大小寫)依次對應1,2,3,…,26,這26個自然數(見表格),當明碼對應的序號x為奇數時,密碼對應的序號![]() ,當明碼對應的序號x為偶數時,密碼對應的序號
,當明碼對應的序號x為偶數時,密碼對應的序號![]() +12,按下述規定,將明碼“love”譯成密碼是( )
+12,按下述規定,將明碼“love”譯成密碼是( )

A.loveB.rkwuC.sdriD.rewj
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某軟件科技公司20人負責研發與維護游戲、網購、視頻和送餐共4款軟件.投入市場后,游戲軟件的利潤占這4款軟件總利潤的40%.如圖是這4款軟件研發與維護人數的扇形統計圖和利潤的條形統計圖.
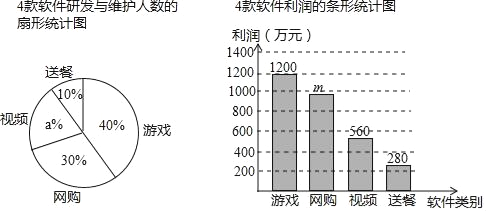
根據以上信息,網答下列問題
(1)直接寫出圖中a,m的值;
(2)分別求網購與視頻軟件的人均利潤;
(3)在總人數和各款軟件人均利潤都保持不變的情況下,能否只調整網購與視頻軟件的研發與維護人數,使總利潤增加60萬元?如果能,寫出調整方案;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
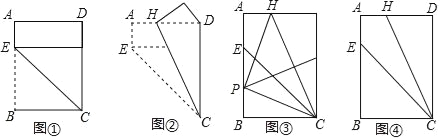
【題目】對給定的一張矩形紙片ABCD進行如下操作:先沿CE折疊,使點B落在CD邊上(如圖①),再沿CH折疊,這時發現點E恰好與點D重合(如圖②)
(1)根據以上操作和發現,求![]() 的值;
的值;
(2)將該矩形紙片展開.
①如圖③,折疊該矩形紙片,使點C與點H重合,折痕與AB相交于點P,再將該矩形紙片展開.求證:∠HPC=90°;
②不借助工具,利用圖④探索一種新的折疊方法,找出與圖③中位置相同的P點,要求只有一條折痕,且點P在折痕上,請簡要說明折疊方法.(不需說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機小張某天上午營運全是在東西走向的政府大道上進行的,如果規定向東為正,向西為負,他這天上午的行程是(單位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)將最后一名乘客送達目的地時,小張距上午出發點的距離是多少千米?在出發點的什么方向?
(2)若汽車耗油量為0.6升/千米,出車時,郵箱有油72.2升,若小張將最后一名乘客送達目的地,再返回出發地,問小張今天上午是否需要加油?若要加油至少需要加多少才能返回出發地?若不用加油,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年5月3日,中國科學院在上海發布了中國首款人工智能芯片:寒武紀(MLU100),該芯片在平衡模式下的等效理論峰值速度達每秒128 000 000 000 000次定點運算,將數
128 000 000 000 000用科學計數法表示為( )
A. 1.28![]() 1014 B. 1.28
1014 B. 1.28![]() 10-14 C. 128
10-14 C. 128![]() 1012 D. 0.128
1012 D. 0.128![]() 1011
1011
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com