
【題目】綜合與探究
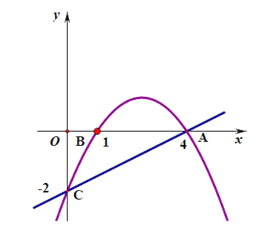
如圖,拋物線y=a![]() 經(jīng)過點(diǎn)A、B、C且點(diǎn)C坐標(biāo)為(0,2).
經(jīng)過點(diǎn)A、B、C且點(diǎn)C坐標(biāo)為(0,2).
(1)求出拋物線的解析式;
(2)在直線AC上方的拋物線上有一點(diǎn)D,使得△DCA的面積最大,求出點(diǎn)D的坐標(biāo).
(3)點(diǎn)H在線段AC上,若OH最短時,在x軸上找一點(diǎn)N,使△CHN周長最小時,求點(diǎn)N的坐標(biāo)
(4)P是拋物線上一動點(diǎn),過P作PM⊥x軸,垂足為M,是否存在P點(diǎn),使得以A,P,M為頂點(diǎn)的三角形與△OAC相似?若存在,請求出符合條件的點(diǎn)P的坐標(biāo);若不存在,請說明理由.
【答案】(1)![]()
(2)D(2,1)
(3)(![]() ,0)
,0)
(4)存在滿足條件的點(diǎn)P,坐標(biāo)為(0,-2)或(2,1)或(5,-2)或(-3,-14).
【解析】
(1)由A、B、C三點(diǎn)的坐標(biāo),利用待定系數(shù)法可求得拋物線解析式;
(2)可以表示出點(diǎn)D的坐標(biāo),過D做DE![]() y軸,交直線AC與點(diǎn)E,表示出DE的長,進(jìn)一步表示出△DCA的面積,利用二次函數(shù)性質(zhì),求出點(diǎn)D坐標(biāo);
y軸,交直線AC與點(diǎn)E,表示出DE的長,進(jìn)一步表示出△DCA的面積,利用二次函數(shù)性質(zhì),求出點(diǎn)D坐標(biāo);
(3)根據(jù)垂線段最短確定點(diǎn)H位置,結(jié)合相似或三角函數(shù),利用將軍飲馬模型,確定點(diǎn)N的位置,并求出其坐標(biāo);
(4)設(shè)出點(diǎn)P的坐標(biāo),表示出PM和AM的長,由三角形相似的性質(zhì)可以得到關(guān)于點(diǎn)P的坐標(biāo)的方程,可求出點(diǎn)P的坐標(biāo).
解:(1)由圖像得拋物線經(jīng)過點(diǎn)A(4,0)、B(1,0)、C (0,2),把A、B、C三點(diǎn)坐標(biāo)代入解析式得: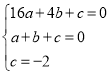 ,解得
,解得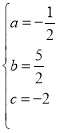 ,
,
∴拋物線解析式為:![]()
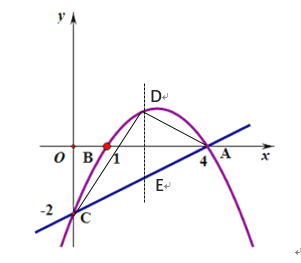
(2)∵D在直線AC上方的拋物線上,
∴設(shè)D坐標(biāo)為(![]() )(0<t<4),
)(0<t<4),
如圖,過D作DE![]() y軸,交直線AC與點(diǎn)E,
y軸,交直線AC與點(diǎn)E,
則點(diǎn)E坐標(biāo)為(![]() ),
),
∴![]()
∴![]()
![]()
![]()
∵-1<0,
∴當(dāng)t=2時,S△DCA有最大值4,此時D坐標(biāo)為(2,1);
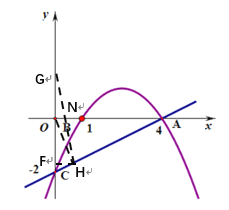
(3)如圖,∵H在AC上,且OH最短,
∴OH為點(diǎn)O到AC的垂線段.
作OH⊥AC垂足為H,作OH⊥y軸,設(shè)點(diǎn)C關(guān)于x軸的對稱點(diǎn)為G,連接HG,交x軸與點(diǎn)N,此時,△CHN周長最小.
∵△CHF∽△CAO,
∴![]()
∵△CHF∽△CHO,
∴![]()
∴![]()
∴![]() ,
,![]() ,
,
∵點(diǎn)G與點(diǎn)C關(guān)于x軸對稱,
∴OG=2
∵△GON∽△GFH,
∴![]()
即: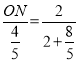 ,解得ON=
,解得ON=![]()
∴點(diǎn)N坐標(biāo)為(![]() ,0);
,0);
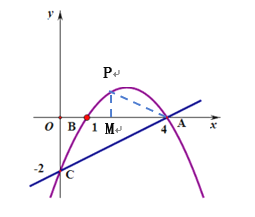
(4)如圖,設(shè)點(diǎn)P的坐標(biāo)為(![]() ),則M坐標(biāo)為(
),則M坐標(biāo)為(![]() ),
),
∴![]() ,
,
![]()
∵A(4,0)、C (0,2),
∴OA=4,OC=2
∵PM⊥x軸,
∴∠PMA=∠COA=90°
∴當(dāng)△PAM和△CAO相似時,有兩種情況.
①當(dāng)![]() 時,
時,![]() ,
,
解得:m=4或m=2,或m=0,
當(dāng)m=4時,點(diǎn)P在x軸上,不合題意,舍去,
當(dāng)m=0時,點(diǎn)P(0,-2),
當(dāng)m=2是,點(diǎn)P(2,1);
②當(dāng)![]() 時,
時,![]() ,
,
解得:m=4或m=5,或m=-3,
當(dāng)m=5時,點(diǎn)P(5,-2),
當(dāng)m=-3時,點(diǎn)P(-3,-14),
綜上所述:存在滿足條件的點(diǎn)P,其坐標(biāo)為(0,-2)或(2,1)或(5,-2)或(-3,-14).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】清清從家步行到公交車站臺,等公交車去學(xué)校.下公交車后又步行了一段路程才到學(xué)校. 圖中的折線表示清清的行程s(米)與所花時間t (分)之間的函數(shù)關(guān)系. 下列說法錯誤的是( )

A. 清清等公交車時間為3分鐘 B. 清清步行的速度是80米/分
C. 公交車的速度是500米/分 D. 清清全程的平均速度為290米/分
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
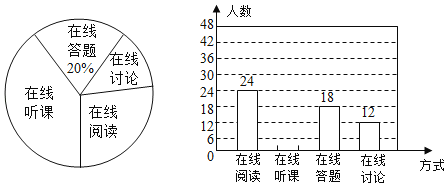
【題目】隨著科技的進(jìn)步和網(wǎng)絡(luò)資源的豐富,在線學(xué)習(xí)已經(jīng)成為更多人的自主學(xué)習(xí)選擇.某校計劃為學(xué)生提供以下四類在線學(xué)習(xí)方式:在線閱讀、在線聽課、在線答題和在線討論.為了解決學(xué)生需求,該校隨機(jī)對本校部分學(xué)生進(jìn)行了“你對哪類在線學(xué)習(xí)方式最感興趣”的調(diào)査,并根據(jù)調(diào)査結(jié)果繪制成如下兩幅不完整的統(tǒng)計圖.請你根據(jù)圖中提供的信息解答下列問題:
(1)在這次調(diào)查中,一共抽取了多少名學(xué)生?
(2)通過計算補(bǔ)全條形統(tǒng)計圖
(3)若該校共有學(xué)生2100人,請你估計該校對在線閱讀最感興趣的學(xué)生有多少名?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校八年級甲、乙兩班各有學(xué)生50人,為了了解這兩個班學(xué)生身體素質(zhì)情況,進(jìn)行了抽樣調(diào)查,過程如下,請補(bǔ)充完整.
(1)收集數(shù)據(jù):從甲、乙兩個班各隨機(jī)抽取10名學(xué)生進(jìn)行身體素質(zhì)測試,測試成績(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述數(shù)據(jù):按如下分?jǐn)?shù)段整理、描述這兩組樣本數(shù)據(jù):
成績x 人數(shù) 班級 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析數(shù)據(jù):
①兩組樣本數(shù)據(jù)的平均數(shù)、中位數(shù)、眾數(shù)如表所示:
班級 | 平均數(shù) | 中位數(shù) | 眾數(shù) |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若規(guī)定測試成績在80分(含80分)以上的學(xué)生身體素質(zhì)為優(yōu)秀,請估計乙班50名學(xué)生中身體素質(zhì)為優(yōu)秀的學(xué)生有______人.
③現(xiàn)從甲班指定的2名學(xué)生(1男1女),乙班指定的3名學(xué)生(2男1女)中分別抽取1名學(xué)生去參加上級部門組織的身體素質(zhì)測試,用樹狀圖和列表法求抽到的2名同學(xué)是1男1女的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,AB=2![]() ,AC=4,BC=2,以AB為邊向△ABC外作△ABD,若△ABD是等腰直角三角形,則線段CD的長為_____.
,AC=4,BC=2,以AB為邊向△ABC外作△ABD,若△ABD是等腰直角三角形,則線段CD的長為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】近年,《中國詩詞大會》、《朗讀者》,《經(jīng)典詠流傳》、《國家寶藏》等文化類節(jié)目相繼走紅,被人們稱為“清流綜藝”,六中上智中學(xué)某興趣小組想了解全校學(xué)生對這四個節(jié)目的喜愛情況,隨機(jī)抽取了部分學(xué)生進(jìn)行調(diào)查統(tǒng)計,要求每名學(xué)生選出一個自己最喜愛的節(jié)目,并將調(diào)查結(jié)果給制成如下統(tǒng)計圖(其中《中國詩詞大會》,《朗讀者》,《經(jīng)典詠流傳》,《國家寶藏》分別用A,B,C.D表示),請你結(jié)合圖中信息解答下列問題:
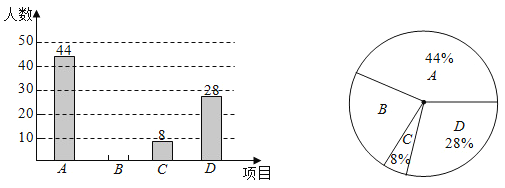
(1)本次調(diào)查的學(xué)生人數(shù)是 人:
(2)請把條形統(tǒng)計圖補(bǔ)充完整.
(3)在扇形統(tǒng)計圖中,B對應(yīng)的圓心角的度數(shù)是 .
(4)已知六中上智中學(xué)共有3200名學(xué)生,請根據(jù)樣本估計全校最喜愛《朗讀者》的人數(shù)是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知△ABC,∠C = 90°,![]() .D為BC上一點(diǎn),且到A,B兩點(diǎn)的距離相等.
.D為BC上一點(diǎn),且到A,B兩點(diǎn)的距離相等.
(1)用直尺和圓規(guī),作出點(diǎn)D的位置(不寫作法,保留作圖痕跡);
(2)連結(jié)AD,若∠B = 35°,求∠CAD的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
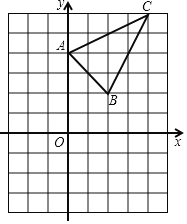
【題目】如圖,△ABC在坐標(biāo)平面內(nèi),三個頂點(diǎn)的坐標(biāo)分別為A(0,4),B(2,2),C(4,6)(正方形網(wǎng)格中,每個小正方形的邊長為1)
(1)畫出△ABC向下平移5個單位得到的△A1B1C1,并寫出點(diǎn)B1的坐標(biāo);
(2)以點(diǎn)O為位似中心,在第三象限畫出△A2B2C2,使△A2B2C2與△ABC位似,且位似比為1:2,直接寫出點(diǎn)C2的坐標(biāo)和△A2B2C2的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知平行四邊形![]() 中,
中,![]() 是
是![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() 并延長,交
并延長,交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() .
.

(1)求證:![]() ;
;
(2)連接![]() ,
,![]() ,當(dāng)
,當(dāng)![]() _______°時,四邊形
_______°時,四邊形![]() 是正方形?
是正方形?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com