
【題目】為迎接十二運,某校開設了A:籃球,B:毽球,C:跳繩,D:健美操四種體育活動,為了解學生對這四種體育活動的喜歡情況,在全校范圍內隨機抽取若干名學生,進行問卷調查(每個被調查的同學必須選擇而且只能在4中體育活動中選擇一種).將數據進行整理并繪制成以下兩幅統計圖(未畫完整).

(1)這次調查中,一共查了 名學生:
(2)請補全兩幅統計圖:
(3)若有3名最喜歡毽球運動的學生,1名最喜歡跳繩運動的學生組隊外出參加一次聯誼互活動,欲從中選出2人擔任組長(不分正副),求兩人均是最喜歡毽球運動的學生的概率.
【答案】(1)200;(2)補圖見解析;(3)![]() .
.
【解析】
(1)根據A類的人數和所占的百分比,即可求出總人數;
(2)用整體1減去A、C、D類所占的百分比,即可求出B所占的百分比;用總人數乘以所占的百分比,求出C的人數,從而補全圖形;
(3)根據題意采用列舉法,舉出所有的可能,注意要做到不重不漏,再根據概率公式即可得出答案.
(1)調查的總學生是![]() =200(名);
=200(名);
故答案為200.
(2)B所占的百分比是1-15%-20%-30%=35%,
C的人數是:200×30%=60(名),
補圖如下:

(3)用A1,A2,A3表示3名喜歡毽球運動的學生,B表示1名跳繩運動的學生,
則從4人中選出2人的情況有:(A1,A2),(A1,A3),(A1,B),(A2,A3),(A2,B),(A3,B),共計6種,
選出的2人都是最喜歡毽球運動的學生有(A1,A2),(A1,A3),(A2,A3)共計3種,
則兩人均是最喜歡毽球運動的學生的概率![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
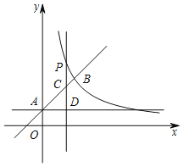
【題目】如圖,直線l:y=x+1與y軸交于點A,與雙曲線![]() (x>0)交于點B(2,a).
(x>0)交于點B(2,a).
(1)求a,k的值.
(2)點P是直線l上方的雙曲線上一點,過點P作平行于y軸的直線,交直線l于點C,過點A作平行于x軸的直線,交直線PC于點D,設點P的橫坐標為m.
①若m=![]() ,試判斷線段CP與CD的數量關系,并說明理由;②若CP>CD,請結合函數圖象,直接寫出m的取值范圍.
,試判斷線段CP與CD的數量關系,并說明理由;②若CP>CD,請結合函數圖象,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
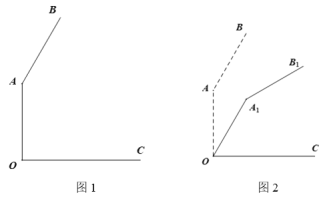
【題目】圖1是某品牌臺燈豎直擺放在水平桌面上的側面示意圖,其中![]() 為桌面(臺燈底座的厚度忽略不計),臺燈支架
為桌面(臺燈底座的厚度忽略不計),臺燈支架![]() 與燈管
與燈管![]() 的長度都為
的長度都為![]() ,且夾角為
,且夾角為![]() (即
(即![]() ),若保持該夾角不變,當支架
),若保持該夾角不變,當支架![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 時,支架與燈管落在
時,支架與燈管落在![]() 位置(如圖2所示),則燈管末梢
位置(如圖2所示),則燈管末梢![]() 的高度會降低_______
的高度會降低_______![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線表達式C:![]() , 已知點A(0,2),點P是拋物線上一點,若Rt△AOP有一個銳角正切值為
, 已知點A(0,2),點P是拋物線上一點,若Rt△AOP有一個銳角正切值為![]() ,則點P的坐標_________________.
,則點P的坐標_________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,∠ACB=30°,將一塊直角三角板的直角頂點P放在兩對角線AC,BD的交點處,以點P為旋轉中心轉動三角板,并保證三角板的兩直角邊分別與邊AB,BC所在的直線相交,交點分別為E,F.
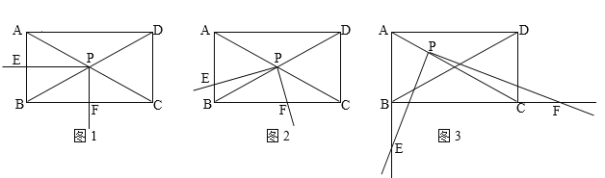
(1)當PE⊥AB,PF⊥BC時,如圖1,則![]() 的值為 ;
的值為 ;
(2)在(1)的基礎上,現將三角板繞點P逆時針旋轉![]() (0°<
(0°<![]() <60°)角,如圖2,求
<60°)角,如圖2,求![]() 的值;
的值;
(3)若與(2)相比只有如下變化,點P在線段AC上,且AP:PC=1:2,旋轉角度![]() ,滿足60°<
,滿足60°<![]() <90°時,即如圖3示,
<90°時,即如圖3示,![]() 的值是否變化?證明你的結論.
的值是否變化?證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
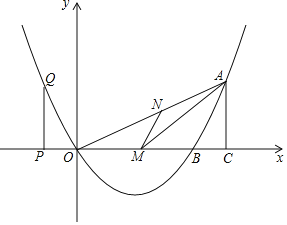
【題目】如圖,已知二次函數的圖象過點O(0,0).A(8,4),與x軸交于另一點B,且對稱軸是直線x=3.
(1)求該二次函數的解析式;
(2)若M是OB上的一點,作MN∥AB交OA于N,當△ANM面積最大時,求M的坐標;
(3)P是x軸上的點,過P作PQ⊥x軸與拋物線交于Q.過A作AC⊥x軸于C,當以O,P,Q為頂點的三角形與以O,A,C為頂點的三角形相似時,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
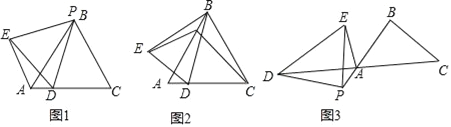
【題目】已知:等邊△ABC的邊長為4,點P在線段AB上,點D在線段AC上,且△PDE為等邊三角形,當點P與點B重合時(如圖1),AD+AE的值為 ;
[類比探究]在上面的問題中,如果把點P沿BA方向移動,使PB=1,其余條件不變(如圖2),AD+AE的值是多少?請寫出你的計算過程;
[拓展遷移]如圖3,△ABC中,AB=BC,∠ABC=a,點P在線段BA延長線上,點D在線段CA延長線上,在△PDE中,PD=PE,∠DPE=a,設AP=m,則線段AD、AE有怎樣的等量關系?請用含m,a的式子直接寫出你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
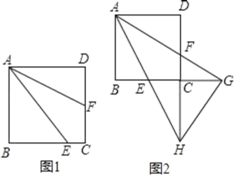
【題目】如圖,正方形ABCD中,E為BC邊上任意點,AF平分∠EAD,交CD于點F.
(1)如圖1,若點F恰好為CD中點,求證:AE=BE+2CE;
(2)在(1)的條件下,求![]() 的值;
的值;
(3)如圖2,延長AF交BC的延長線于點G,延長AE交DC的延長線于點H,連接HG,當CG=DF時,求證:HG⊥AG.
查看答案和解析>>
科目:初中數學 來源: 題型:
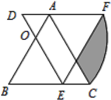
【題目】△ABC為等邊三角形,點O為AB邊上一點,且BO=2AO=4,將△ABC繞點O逆時針旋轉60°得△DEF,則圖中陰影部分的面積為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com