
【題目】某企業為了解飲料自動售賣機的銷售情況,對甲、乙兩個城市的飲料自動售賣機進行抽樣調查,從兩個城市中所有的飲料自動售賣機中分別抽取16臺,記錄下某一天各自的銷售情況(單位:元)如下:
甲:25、45、38、22、10、28、61、18、38、45、78、45、58、32、16、78
乙:48、52、21、25、33、12、42、39、41、42、33、44、33、18、68、72
整理、描述數據:對銷售金額進行分組,各組的頻數如下:
銷傳金額 |
|
|
|
|
甲 | 3 | 6 | 4 | 3 |
乙 | 2 | 6 | a | b |
分析數據:兩組樣本數據的平均數、中位數如下表所示:
城市 | 中位數 | 平均數 | 眾數 |
甲 | C | 39.8 | 45 |
乙 | 40 | 38.9 | d |
請根據以上信息,回答下列問題:
(1)填空:a=, b=, c=, d=.
(2)兩個城市目前共有飲料自動售賣機4000臺,估計日銷售金額不低于40元的數量約為多少臺?
(3)根據以上數據,你認為甲、乙哪個城市的飲料自動售賣機銷售情況較好?請說明理由(一條理由即可).
【答案】(1)6,2,38,33 (2)1875 (3)見解析(答案不唯一)
【解析】
(1)根據某一天各自的銷售情況求出![]() 的值,根據中位數的定義求出
的值,根據中位數的定義求出![]() 的值,根據眾數的定義求出
的值,根據眾數的定義求出![]() 的值.
的值.
(2)用樣本估算整體的方法去計算即可.
(3)根據平均數、眾數、中位數的性質判斷即可.
(1)![]() .
.
(2)![]() (臺)
(臺)
故估計日銷售金額不低于40元的數量約為1875臺.
(3)可以推斷出甲城市的飲料自動售貨機銷售情況較好,理由如下:
①甲城市飲料自動售貨機銷售金額的平均數較高,表示甲城市的銷售情況較好;
②甲城市飲料自動售貨機銷售金額的眾數較高,表示甲城市的銷售金額較高;
可以推斷出乙城市的飲料自動售貨機銷售情況較好,理由如下:
①乙城市飲料自動售貨機銷售金額的中位數較高,表示乙城市銷售金額高的自動售貨機數量較多;


科目:初中數學 來源: 題型:
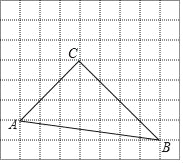
【題目】如圖,在每個小正方形的邊長為1的網格中,△ABC的頂點A,B,C均在格點上.
(1)∠ACB的大小為 (度)
(2)在如圖所示的網格中,以A為中心,取旋轉角等于∠BAC,把△ABC逆時針旋轉,請用無刻度的直尺,畫出旋轉后的△ABC,并簡要說明旋轉后點C和點B的對應點點C′和點B′的位置是如何而找到的(不要求證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
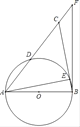
【題目】如圖,在等腰△ABC中,AB=BC,以AB為直徑的半圓分別交AC、BC于點D、E兩點,BF與⊙O相切于點B,交AC的延長線于點F.
(1)求證:D是AC的中點;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】佳佳調査了七年級400名學生到校的方式,根據調查結果繪制出統計圖的一部分如圖:
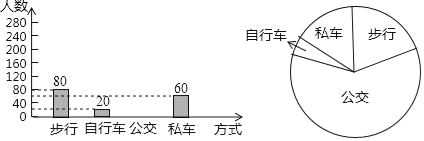
(1)補全條形統計圖;
(2)求扇形統計圖中表示“步行”的扇形圓心角的度數;
(3)估計在3000名學生中乘公交的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“小組合作制”正在七年級如火如茶地開展,旨在培養七年級學生的合作學習的精神和能力,學會在合作中自主探索.數學課上,吳老師在講授“角平分線”時,設計了如下四種教學方法:①教師講授,學生練習;②學生合作交流,探索規律;③教師引導學生總結規律,學生練習;④教師引導學生總結規律,學生合作交流,吳老師將上述教學方法作為調研內容發到七年級所有同學手中要求每位同學選出自己最喜歡的一種,然后吳老師從所有調查問卷中隨機抽取了若干份調查問卷作為樣本,統計如下:
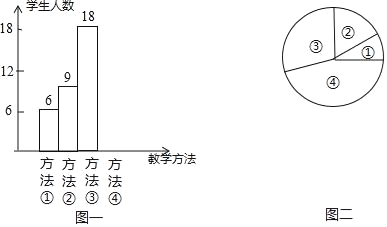
序號①②③④代表上述四種教學方法,圖二中,表示①部分的扇形的中心角度數為36°,請回答問題:
(1)在后來的抽樣調查中,吳老師共抽取 位學生進行調查;并將條形統計圖補充完整;
(2)圖二中,表示③部分的扇形的中心角為多少度?
(3)若七年級學生中選擇④種教學方法的有540人,請估計七年級總人數約為多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,熱氣球的探測器顯示,從熱氣球A看一棟大樓頂部B的俯角為![]() ,看這棟大樓底部C的俯角為
,看這棟大樓底部C的俯角為![]() ,熱氣球A的高度為270米,則這棟大樓的高度為______米
,熱氣球A的高度為270米,則這棟大樓的高度為______米![]()

查看答案和解析>>
科目:初中數學 來源: 題型:
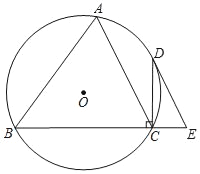
【題目】如圖,△ABC內接于⊙O,過點C作BC的垂線交⊙O于D,點E在BC的延長線上,且∠DEC=∠BAC.
(1)求證:DE是⊙O的切線;
(2)若AC∥DE,當AB=8,CE=2時,求⊙O直徑的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ABC=90°,以AB為直徑的⊙O交AC于點D,E是BC的中點,連接DE、OE.
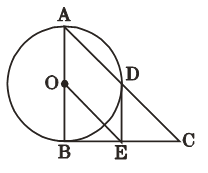
(1)判斷DE與⊙O的位置關系并說明理由;
(2)求證:![]()
(3)若tanC=![]() ,DE=2,求AD的長.
,DE=2,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
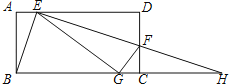
【題目】如圖,將矩形ABCD的一個角翻折,使得點D恰好落在BC邊上的點G處,折痕為EF,若EB為∠AEG的平分線,EF和BC的延長線交于點H.下列結論中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面積相等;⑤若![]() ,則
,則![]() .以上命題,正確的有( )
.以上命題,正確的有( )
A.2個B.3個C.4個D.5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com