
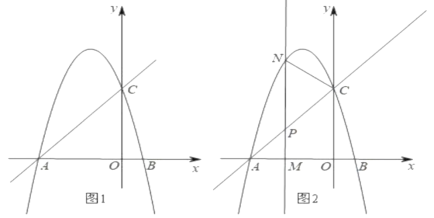
【題目】如圖1,直線y=x+c與x軸交于點A(-3,0),與y軸交于點C,拋物線y=-x2+bx+c經過點A、C.
(1)求拋物線的解析式;
(2)如圖2所示,M是線段0A上一個動點,過點M垂直于x軸的直線與直線AC和拋物線分別交于點P、N.若以C、P、N為頂點的三角形與△APM相似,求四邊形MNCO的面積.
【答案】(1)y=-x2-2x+3;(2)6或![]()
【解析】
(1)將A代入y=x+c求出c,從而求出C點坐標,再將A、C點代入y=-x2+bx+c算出解析式即可;
(2)△APM是直角三角形且![]() ,根據C、P、N為頂點的三角形與△APM相似分為
,根據C、P、N為頂點的三角形與△APM相似分為![]() 或
或![]() 進行分類討論求出M、N點的坐標再求算四邊形MNCO的面積即可.
進行分類討論求出M、N點的坐標再求算四邊形MNCO的面積即可.
解:(1)∵直線y=x+c與x軸交于點A(-3,0),將A(-3,0)代入得:c=3
∴直線解析式為:y=x+3
∴C(0,3)
將A(-3,0),C(0,3)代入y=-x2+bx+c得:
![]() 解得:
解得:![]()
∴拋物線的解析式為:y=-x2-2x+3
(2)設![]()
由題可知:![]() 是直角三角形且
是直角三角形且![]() ,要使C、P、N為頂點的三角形與△APM相似
,要使C、P、N為頂點的三角形與△APM相似
①當![]() ,如圖:
,如圖:
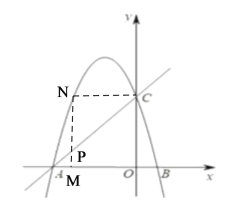
此時C、N在一條直線上
∴![]()
∴四邊形MNCO的面積=![]()
②![]() 時,如圖:
時,如圖:
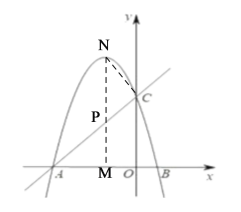
![]() 得出:
得出:![]() 解得:
解得:![]()
∴![]()
∴四邊形MNCO的面積=![]()
綜上所述:若以C、P、N為頂點的三角形與△APM相,四邊形MNCO的面積為6或![]() .
.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:初中數學 來源: 題型:
【題目】天門山索道是世界最長的高山客運索道,位于張家界天門山景區.在一次檢修維護中,檢修人員從索道A處開始,沿A﹣B﹣C路線對索道進行檢修維護.如圖:已知![]() 米,
米,![]() 米,AB與水平線
米,AB與水平線![]() 的夾角是
的夾角是![]() ,BC與水平線
,BC與水平線![]() 的夾角是
的夾角是![]() .求:本次檢修中,檢修人員上升的垂直高度
.求:本次檢修中,檢修人員上升的垂直高度![]() 是多少米?(結果精確到1米,參考數據:
是多少米?(結果精確到1米,參考數據:![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠ACB=45°,點D為射線BC上一動點(與點B、C不重合),連接AD,以AD為一邊在AD一側作正方形ADEF(如圖1).
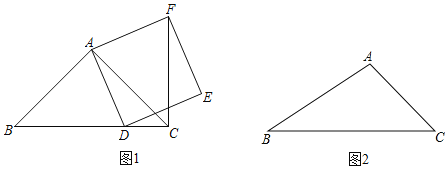
(1)如果AB=AC,且點D在線段BC上運動,證明:CF⊥BD;
(2)如果AB≠AC,且點D在線段BC的延長線上運動,請在圖2中畫出相應的示意圖,此時(1)中的結論是否成立?請說明理由;
(3)設正方形ADEF的邊DE所在直線與直線CF相交于點P,若AC=4,CD=2,求線段CP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() 是平面內不與點
是平面內不與點![]() 重合的任意一點,連接
重合的任意一點,連接![]() ,將線段
,將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到線段
得到線段![]() ,連接
,連接![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 的中點.
的中點.
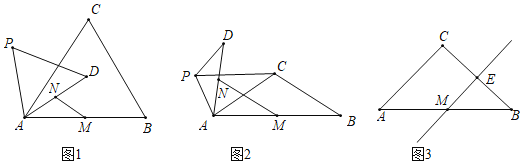
(1)問題發現:
如圖1,當![]() 時,
時,![]() 的值是_________,直線
的值是_________,直線![]() 與直線
與直線![]() 相交所成的較小角的度數是________.
相交所成的較小角的度數是________.
(2)類比探究:
如圖2,當![]() 時,請寫出
時,請寫出![]() 的值及直線
的值及直線![]() 與直線
與直線![]() 相交所成的較小角的度數,并說明理由.
相交所成的較小角的度數,并說明理由.
(3)解決問題:
如圖3,當![]() 時,若
時,若![]() 是
是![]() 的中點,點
的中點,點![]() 在直線
在直線![]() 上,且點
上,且點![]() 在同一條直線上,請直接寫出
在同一條直線上,請直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形網格中建立平面直角坐標系,已知△ABC三個頂點分別為A(﹣1,2)、B(2,1)、C(4,5).
(1)畫出△ABC關于x對稱的△A1B1C1;
(2)以原點O為位似中心,在x軸的上方畫出△A2B2C2,使△A2B2C2與△ABC位似,且位似比為2,并求出△A2B2C2的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個服裝廠加工同種型號的防護服,甲廠每天加工的數量是乙廠每天加工數量的1.5倍,兩廠各加工450套防護服,甲廠比乙廠要少用3天.
(1)求甲、乙兩廠每天各加工多少套防護服?
(2)已知甲、乙兩廠加工這種防護服每天的費用分別是180元和160元,疫情期間,某醫院緊急需要2400套這種防護服,甲廠單獨加工一段時間后另有安排,剩下任務只能由乙單獨完成.如果總加工費不超過6000元,那么甲廠至少要加工多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年我國許多地方嚴重的“旱情”,為了鼓勵居民節約用水,區政府計劃實行兩級收費制,即每月用水量不超過14噸(含14噸)時,每噸按政府補貼優惠價收費;每月超過14噸時,超過部分每噸按市場調節價收費.小英家1月份用水20噸,交水費29元;2月份用水18噸,交水費24元.
(1)求每噸水的政府補貼優惠價和市場調節價分別是多少?
(2)設每月用水量為x噸,應交水費為y元,寫出y與x之間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明隨機調查了若干市民租用公共自行車的騎車時間t(單位:分),將獲得的數據分成四組,繪制了如下統計圖。請根據圖中信息,解答下列問題:
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922393511583744/1923977001213952/STEM/d5900c7cb9b84a9a89aefef7d82bcf93.png]
(1)這次被調查的總人數是多少?
(2)試求表示A組的扇形圓心角的度數,并補全條形統計圖;
(3)如果騎自行車的平均速度為12km/h,請估算,在租用公共自行車的市民中,騎車路程不超過6km的人數所占的百分比。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經過點A(﹣1,0),B(4,0),C(0,2)三點,點D與點C關于x軸對稱,點P是x軸上的一個動點,設點P的坐標為(m,0),過點P做x軸的垂線l交拋物線于點Q,交直線BD于點M.
(1)求該拋物線所表示的二次函數的表達式;
(2)已知點F(0,![]() ),當點P在x軸上運動時,試求m為何值時,四邊形DMQF是平行四邊形?
),當點P在x軸上運動時,試求m為何值時,四邊形DMQF是平行四邊形?
(3)點P在線段AB運動過程中,是否存在點Q,使得以點B、Q、M為頂點的三角形與△BOD相似?若存在,求出點Q的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com