
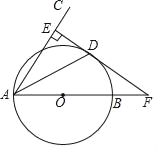
【題目】如圖,AB是⊙O的直徑,弦AD平分∠BAC,過點D作DE⊥AC于E.
(1)求證:ED是⊙O的切線;
(2)若ED,AB的延長線相交于F,且AE=5,EF=12,求BF的長.
【答案】(1)證明見解析;(2)BF=![]() .
.
【解析】試題分析:(1)連接OD,推出∠ODA=∠OAD=∠EAD,推出OD∥AE,推出OD⊥DE,根據切線的判定推出即可;
(2)在Rt△AEF中,根據勾股定理求得AF=13,設⊙O的半徑為r,則有OD=r,OF=13﹣r,BF=AF﹣AB=13﹣2r,通過證明△OFD∽△AFE,根據相似三角形對應邊成比例進而求得r的值即可得..
試題解析:(1)如圖,∵DE⊥AC,
∴∠AEF=90°
連接OD,
∴OA=OD,
∴∠OAD=∠ODA,
∵AD是∠BAC的平分線,
∴∠DAC=∠DAB,
∴∠DAE=∠ODA,
∴OD∥AE,
∴∠ODF=∠AEF=90°,
∴OD⊥EF,
∵點D在⊙O上,
∴ED是⊙O的切線;
(2)在Rt△AEF中,根據勾股定理得,AF=![]() =13,
=13,
設⊙O的半徑為r,
∴OD=r,OF=13﹣r,BF=AF﹣AB=13﹣2r,
由(1)知,OD∥AE,
∴△OFD∽△AFE,
∴![]() ,
,
∴![]() ,
,
∴r=![]() ,
,
∴BF=13﹣r=![]() .
.


科目:初中數學 來源: 題型:
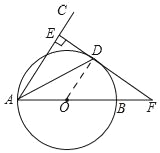
【題目】如圖1,在矩形ABCD中,動點E從A出發,沿![]() 方向運動,當點E到達點C時停止運動,過點E做
方向運動,當點E到達點C時停止運動,過點E做![]() ,交CD于F點,設點E運動路程為x,
,交CD于F點,設點E運動路程為x, ![]() ,如圖2所表示的是y與x的函數關系的大致圖象,當點E在BC上運動時,FC的最大長度是
,如圖2所表示的是y與x的函數關系的大致圖象,當點E在BC上運動時,FC的最大長度是![]() ,則矩形ABCD的面積是( )
,則矩形ABCD的面積是( )
A. ![]() B.
B. ![]() C. 6 D. 5
C. 6 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
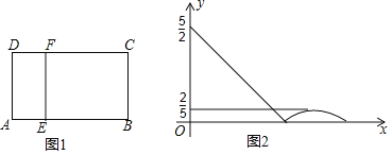
【題目】將正方形 ABCD (如圖 1)作如下劃分:
第1次劃分:分別連接正方形ABCD對邊的中點(如圖2),得線段HF和EG,它們交于點M,此時圖2中共有5個正方形;
第2次劃分:將圖2 左上角正方形AEMH再作劃分,得圖3,則圖3 中共有9個正方形;
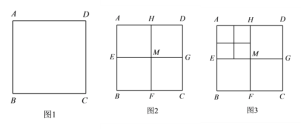
(1)若每次都把左上角的正方形依次劃分下去,則第100次劃分后,圖中共有 個正方形;
(2)繼續劃分下去,第幾次劃分后能有805個正方形?寫出計算過程.
(3)按這種方法能否將正方形ABCD劃分成有2015個正方形的圖形?如果能,請算出是第幾次劃分,如果不能,需說明理由.
(4)如果設原正方形的邊長為1,通過不斷地分割該面積為1的正方形,并把數量關系和幾何圖形巧妙地結合起來,可以很容易得到一些計算結果,試著探究求出下面表達式的結果吧.
計算 ![]() .( 直接寫出答案即可)
.( 直接寫出答案即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】嘉興某校組織了“垃圾分類”知識競賽活動,獲獎同學在競賽中的成績繪成如下圖表,
根據圖表提供的信息解答下列問題:
垃圾分類知識競賽活動成績統計表
分數段 | 頻數 | 頻數頻率 |
80≤x<85 | x | 0.2 |
85≤x<90 | 80 | y |
90≤x<95 | 60 | 0.3 |
95≤x<100 | 20 | 0.1 |
(1)求本次獲獎同學的人數;
(2)求表中x,y的數值:并補全頻數分布直方圖.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠A=∠ABC=90°,E是邊CD的中點,連接BE并延長與AD的延長線相交于點F,連接CF.四邊形BDFC是平行四邊形嗎?證明你的結論.
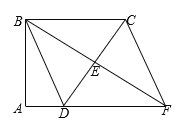
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機沿東西方向的公路送旅客,如果約定向東為正,向西為負,當天的歷史記錄如下(單位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)出租車司機最后到達的地方在出發點的哪個方向?距出發點多遠?
(2)出租車司機最遠離出發點有多遠?
(3)若汽車每千米耗油量為![]() 升,則這天共耗油多少升?
升,則這天共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠在生產過程中要消耗大量電能,消耗每千度電產生利潤與電價是一次函數關系,經過測算,工廠每千度電產生利潤y(元/千度))與電價x(元/千度)的函數圖象如圖:
(1)請求出y與x之間的函數關系式;
(2)為了實現節能減排目標,有關部門規定,該廠電價x(元/千度)與每天用電量m(千度)的函數關系為x=20m+500,且該工廠每天用電量不超過50千度,為了獲得最大利潤w,工廠每天應安排使用多少度電?工廠每天消耗電產生利潤最大是多少元?
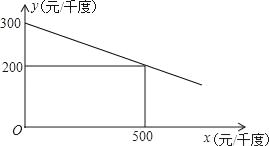
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com