
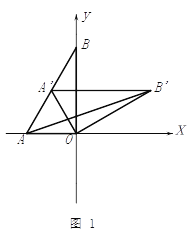
【題目】如圖1,在平面直角坐標系, ![]() 為坐標原點,點
為坐標原點,點![]() ,點
,點![]() .
.
(1)求![]() 的度數;
的度數;
(2)如圖1,將⊿![]() 繞點
繞點![]() 順時針得⊿
順時針得⊿![]() ,當
,當![]() 恰好落在
恰好落在![]() 邊上時,設⊿
邊上時,設⊿![]() 的面積為
的面積為![]() ,⊿
,⊿![]() 的面積為
的面積為![]() ,
,![]() 與
與![]() 有何關系?為什么?
有何關系?為什么?
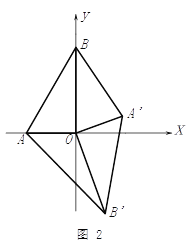
(3)若將⊿![]() 繞點
繞點![]() 順時針旋轉到如圖2所示的位置,
順時針旋轉到如圖2所示的位置, ![]() 與
與![]() 的關系發生變化了嗎?證明你的判斷.
的關系發生變化了嗎?證明你的判斷.
【答案】(1)![]() ;
;
(2)![]() ,理由見解析;
,理由見解析;
(3)![]() 與
與![]() 的關系沒變,即
的關系沒變,即![]() ,理由見解析.
,理由見解析.
【解析】試題分析:本題的⑴問求![]() 的度數化歸在
的度數化歸在![]() △
△![]() 來解決,根據點
來解決,根據點![]() ,點
,點![]() 容易求出
容易求出![]() 的長度,利用三角函數的定義計算出三角函數值,從而求出該角的度數.
的長度,利用三角函數的定義計算出三角函數值,從而求出該角的度數.
本題的⑵問抓住⊿![]() 和⊿
和⊿![]() 的邊
的邊![]() 是同一三角形⊿
是同一三角形⊿![]() 的邊;根據旋轉的特征可以推出
的邊;根據旋轉的特征可以推出![]() ,結合⑴問容易推出三角形⊿
,結合⑴問容易推出三角形⊿![]() 是等邊三角形,等邊三角形不但三邊相等,而且三邊上的高也是相等的,我們利用“等底等高的三角形”的結論容易判斷出
是等邊三角形,等邊三角形不但三邊相等,而且三邊上的高也是相等的,我們利用“等底等高的三角形”的結論容易判斷出![]() .
.
本題的⑶問也抓住根據旋轉的特征可以推出⊿![]() 和⊿
和⊿![]() 的邊
的邊![]() ;其實我們只需找到
;其實我們只需找到![]() 邊上高相等;而
邊上高相等;而![]() 邊上的高可以化在兩個三角形中,通過全等三角形可以證得其高相等,再利用“等底等高的三角形”的結論容易判斷出
邊上的高可以化在兩個三角形中,通過全等三角形可以證得其高相等,再利用“等底等高的三角形”的結論容易判斷出![]() .(本問也可以用相似形的相關知識使問題獲得解決.)
.(本問也可以用相似形的相關知識使問題獲得解決.)
試題解析:(1)∵點![]() ,點
,點![]()
∴![]()
又![]()
∴![]()
∴![]()
(2)![]() .
.
理由如下:

根據旋轉的征可知: ![]() .又
.又![]()
∴⊿![]() 是等邊三角形
是等邊三角形
∴![]()
∴![]() ∥
∥![]() 軸
軸
∴點![]() 到
到![]() 軸的距離相等(圖中
軸的距離相等(圖中![]() )
)
∵等邊⊿![]() 的三條高都相等(圖中
的三條高都相等(圖中![]() )
)
∴點![]() 到
到![]() 的距離等于點
的距離等于點![]() 到
到![]() 軸的距離(圖中
軸的距離(圖中![]() )
)
∴![]() (等底等高的三角形面積相等)
(等底等高的三角形面積相等)
(3)![]() 與
與![]() 的關系沒變,即
的關系沒變,即![]() .
.
理由如下:
過點作![]() 于
于![]() ,過點
,過點![]() 作
作![]()
![]() 于
于![]() .
.

∴![]()
根據題意可知: ![]()
根據旋轉的征可知: ![]()
∴![]()
∴![]()
∴⊿![]() ≌⊿
≌⊿![]() (
(![]() )
)
∴![]()
又∵![]()
∴![]() (等底等高的三角形面積相等)
(等底等高的三角形面積相等)


 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AD=5,AB=8,點E為射線DC上一個動點,把△ADE沿直線AE折疊,當點D的對應點F剛好落在線段AB的垂直平分線上時,則DE的長為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列分解因式正確的是( )
A.﹣a+a3=﹣a(1+a2)
B.2a﹣4b+2=2(a﹣2b)
C.a2﹣4=(a﹣2)2
D.a2﹣2a+1=(a﹣1)2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在坐標系中放置一菱形OABC,已知∠ABC=60°,點B在y軸上,OA=1,先將菱形OABC沿x軸的正方向無滑動翻轉,每次翻轉60°,連續翻轉2017次,點B的落點依次為B1,B2,B3,…,則B2017的坐標為( )

A. (1345,0) B. (1345.5,![]() ) C. (1345,
) C. (1345,![]() ) D. (1345.5,0)
) D. (1345.5,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
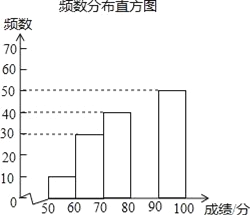
【題目】中華文明,源遠流長;中華漢字,寓意深廣,為了傳承優秀傳統文化,某校團委組織了一次全校3000名學生參加的“漢字聽寫”大賽,賽后發現所有參賽學生的成績均不低于50分,為了更好地了解本次大賽的成績分布情況,隨機抽取了其中200名學生的成績(成績x取整數,總分100分)作為樣本進行整理,得到下列不完整的統計圖表:
成績x/分 | 頻數 | 頻率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
請根據所給信息,解答下列問題:
(1)m= ,n= ;
(2)請補全頻數分布直方圖;
(3)這次比賽成績的中位數會落在 分數段;
(4)若成績在90分以上(包括90分)的為“優”等,則該校參加這次比賽的3000名學生中成績“優”等約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中,點P(-2,3)關于x軸對稱的點的坐標為( )
A. (3,-2) B. (2,-3) C. (-3,2) D. (-2,-3)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com