
【題目】如圖,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,都是一邊在
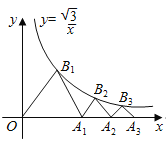
,都是一邊在![]() 軸上的等邊三角形,點(diǎn)
軸上的等邊三角形,點(diǎn)![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都在反比例函數(shù)
都在反比例函數(shù)![]() 的圖象上,點(diǎn)
的圖象上,點(diǎn)![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,都在
,都在![]() 軸上,則
軸上,則![]() 的坐標(biāo)為________.
的坐標(biāo)為________.
【答案】![]()
【解析】
如圖,過(guò)點(diǎn)B1作B1C⊥x軸于點(diǎn)C,過(guò)點(diǎn)B2作B2D⊥x軸于點(diǎn)D,過(guò)點(diǎn)B3作B3E⊥x軸于點(diǎn)E,先在△OCB1中,表示出OC和B1C的長(zhǎng)度,表示出B1的坐標(biāo),代入反比例函數(shù),求出OC的長(zhǎng)度和OA1的長(zhǎng)度,表示出A1的坐標(biāo),同理可求得A2、A3的坐標(biāo),即可發(fā)現(xiàn)一般規(guī)律.
如圖,過(guò)點(diǎn)B1作B1C⊥x軸于點(diǎn)C,過(guò)點(diǎn)B2作B2D⊥x軸于點(diǎn)D,過(guò)點(diǎn)B3作B3E⊥x軸于點(diǎn)E,
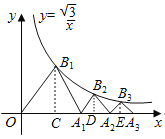
∵△OA1B1為等邊三角形,
∴∠B1OC=60°,
∴![]() ,B1C=
,B1C= ![]() OC,
OC,
設(shè)OC的長(zhǎng)度為x,則B1的坐標(biāo)為(![]() ),代入函數(shù)關(guān)系式可得:
),代入函數(shù)關(guān)系式可得:![]() ,
,
解得,x=1或x=-1(舍去),
∴OA1=2OC=2,
∴A1(2,0)
設(shè)A1D的長(zhǎng)度為y,同理,B2D為![]() y,B2的坐標(biāo)表示為
y,B2的坐標(biāo)表示為![]() ,
,
代入函數(shù)關(guān)系式可得![]() ,
,
解得:y=![]() 或y=
或y=![]() (舍去)
(舍去)
∴A1D=![]() ,A1A2=
,A1A2=![]() ,OA2=
,OA2=![]()
∴A2(![]() ,0)
,0)
設(shè)A2E的長(zhǎng)度為z,同理,B3E為![]() z,B3的坐標(biāo)表示為
z,B3的坐標(biāo)表示為![]() ,
,
代入函數(shù)關(guān)系式可得![]() ,
,
解得:z=![]() 或z=
或z=![]() (舍去)
(舍去)
∴A2E=![]() ,A2A3=
,A2A3=![]() ,OA3=
,OA3=![]()
∴A3(![]() ,0),
,0),
綜上可得:An(![]() ,0),
,0),
故答案為:![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某體育器材專(zhuān)賣(mài)柜經(jīng)銷(xiāo)A、B兩種器材,A種器材每件進(jìn)價(jià)350元,售價(jià)480元;B種器材每件進(jìn)價(jià)200元,售價(jià)300元.
(1)該專(zhuān)賣(mài)柜計(jì)劃用8000元去購(gòu)進(jìn)A、B兩種器材若干件.
①若購(gòu)進(jìn)A種器材x件,B種器材y件,所獲利潤(rùn)w元,請(qǐng)寫(xiě)出w與x之間滿(mǎn)足的函數(shù)關(guān)系式;
②怎樣購(gòu)進(jìn)才能使專(zhuān)賣(mài)柜經(jīng)銷(xiāo)這兩種器材所獲利潤(rùn)最大(其中A種器材不少于7件)?
(2)在“五·一”期間,該專(zhuān)賣(mài)柜對(duì)A、B兩種器材進(jìn)行如下優(yōu)惠促銷(xiāo)活動(dòng):
一次性購(gòu)物總金額 | 優(yōu)惠措施 |
不超過(guò)3000元 | 不優(yōu)惠 |
超過(guò)3000元不超過(guò)4000元 | 售價(jià)打八折 |
超過(guò)4000元 | 售價(jià)打七折 |
促銷(xiāo)活動(dòng)期間:甲學(xué)校去該專(zhuān)賣(mài)柜購(gòu)買(mǎi)A種器材付款2688元;乙學(xué)校去該專(zhuān)賣(mài)柜購(gòu)買(mǎi)B種器材付款2100元,求丙學(xué)校決定一次性購(gòu)買(mǎi)甲學(xué)校和乙學(xué)校購(gòu)買(mǎi)的同樣多的器材需付款多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
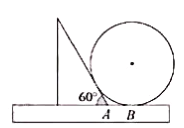
【題目】如圖,一把直尺,![]() 的直角三角板和光盤(pán)如圖擺放,
的直角三角板和光盤(pán)如圖擺放,![]() 為
為![]() 角與直尺交點(diǎn),
角與直尺交點(diǎn),![]() ,則光盤(pán)的直徑是( )
,則光盤(pán)的直徑是( )
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形![]() 是正方形,點(diǎn)
是正方形,點(diǎn)![]() 為對(duì)角線(xiàn)
為對(duì)角線(xiàn)![]() 的中點(diǎn).
的中點(diǎn).
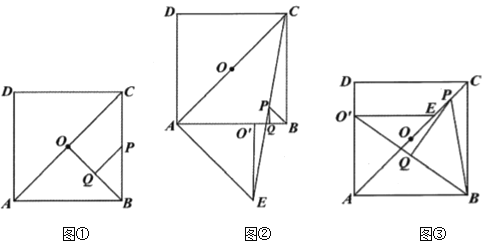
(1)問(wèn)題解決:如圖①,連接![]() ,分別取
,分別取![]() ,
,![]() 的中點(diǎn)
的中點(diǎn)![]() ,
,![]() ,連接
,連接![]() ,則
,則![]() 與
與![]() 的數(shù)量關(guān)系是_____,位置關(guān)系是____;
的數(shù)量關(guān)系是_____,位置關(guān)系是____;
(2)問(wèn)題探究:如圖②,![]() 是將圖①中的
是將圖①中的![]() 繞點(diǎn)
繞點(diǎn)![]() 按順時(shí)針?lè)较蛐D(zhuǎn)
按順時(shí)針?lè)较蛐D(zhuǎn)![]() 得到的三角形,連接
得到的三角形,連接![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,
,![]() .判斷
.判斷![]() 的形狀,并證明你的結(jié)論;
的形狀,并證明你的結(jié)論;
(3)拓展延伸:如圖③,![]() 是將圖①中的
是將圖①中的![]() 繞點(diǎn)
繞點(diǎn)![]() 按逆時(shí)針?lè)较蛐D(zhuǎn)
按逆時(shí)針?lè)较蛐D(zhuǎn)![]() 得到的三角形,連接
得到的三角形,連接![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,
,![]() .若正方形
.若正方形![]() 的邊長(zhǎng)為1,求
的邊長(zhǎng)為1,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,已知△ABC,∠ABC=90°,頂點(diǎn)A在第一象限,B、C在x軸的正半軸上(C在B的右側(cè)),BC=3,AB=4,若雙曲線(xiàn)![]() 交邊AB于點(diǎn)E,交邊AC于中點(diǎn)D.
交邊AB于點(diǎn)E,交邊AC于中點(diǎn)D.
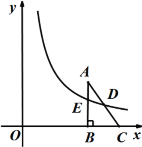
(1)若OB=2,求k;
(2)若AE=![]() , 求直線(xiàn)AC的解析式.
, 求直線(xiàn)AC的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,拋物線(xiàn)![]() 與x軸相交于A、B兩點(diǎn),與y軸相交于點(diǎn)C,點(diǎn)M為拋物線(xiàn)的頂點(diǎn).
與x軸相交于A、B兩點(diǎn),與y軸相交于點(diǎn)C,點(diǎn)M為拋物線(xiàn)的頂點(diǎn).
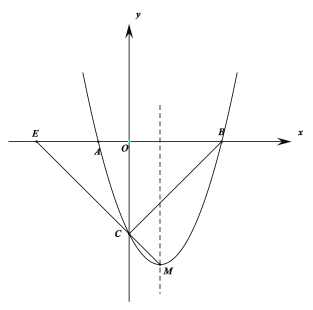
(1)求點(diǎn)C及頂點(diǎn)M的坐標(biāo).
(2)若點(diǎn)N是第四象限內(nèi)拋物線(xiàn)上的一個(gè)動(dòng)點(diǎn),連接![]() 求
求![]() 面積的最大值及此時(shí)點(diǎn)N的坐標(biāo).
面積的最大值及此時(shí)點(diǎn)N的坐標(biāo).
(3)若點(diǎn)D是拋物線(xiàn)對(duì)稱(chēng)軸上的動(dòng)點(diǎn),點(diǎn)G是拋物線(xiàn)上的動(dòng)點(diǎn),是否存在以點(diǎn)B、C、D、G為頂點(diǎn)的四邊形是平行四邊形.若存在,求出點(diǎn)G的坐標(biāo);若不存在,試說(shuō)明理由.
(4)直線(xiàn)CM交x軸于點(diǎn)E,若點(diǎn)P是線(xiàn)段EM上的一個(gè)動(dòng)點(diǎn),是否存在以點(diǎn)P、E、O為頂點(diǎn)的三角形與![]() 相似.若存在,求出點(diǎn)P的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
相似.若存在,求出點(diǎn)P的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】圖①是甘肅省博物館的鎮(zhèn)館之寶——銅奔馬,又稱(chēng)“馬踏飛燕”,于1969年10月出土于武威市的雷臺(tái)漢墓,1983年10月被國(guó)家旅游局確定為中國(guó)旅游標(biāo)志,在很多旅游城市的廣場(chǎng)上都有“馬踏飛燕”雕塑,某學(xué)習(xí)小組把測(cè)量本城市廣場(chǎng)的“馬踏飛燕”雕塑(圖②)最高點(diǎn)離地面的高度作為一次課題活動(dòng),同學(xué)們制定了測(cè)量方案,并完成了實(shí)地測(cè)量,測(cè)得結(jié)果如下表:
課題 | 測(cè)量“馬踏飛燕”雕塑最高點(diǎn)離地面的高度 | |||
測(cè)量示意圖 |
| 如圖,雕塑的最高點(diǎn) | ||
測(cè)量數(shù)據(jù) |
|
|
| 儀器 |
|
| 5米 |
| |
請(qǐng)你根據(jù)上表中的測(cè)量數(shù)據(jù),幫助該小組求出“馬踏飛燕”雕塑最高點(diǎn)離地面的高度(結(jié)果保留一位小數(shù)).(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】房山某中學(xué)改革學(xué)生的學(xué)習(xí)模式,變“老師要學(xué)生學(xué)習(xí)”為“學(xué)生自主學(xué)習(xí)”,培養(yǎng)了學(xué)生自主學(xué)習(xí)的能力.小華與小明同學(xué)就“最喜歡哪種學(xué)習(xí)方式”隨機(jī)調(diào)查了他們周?chē)囊恍┩瑢W(xué),根據(jù)收集到的數(shù)據(jù)繪制了以下的兩個(gè)統(tǒng)計(jì)圖.請(qǐng)根據(jù)下面兩個(gè)不完整的統(tǒng)計(jì)圖回答以下問(wèn)題:

(1)這次抽樣調(diào)查中,共調(diào)查了 名學(xué)生;
(2)補(bǔ)全兩幅統(tǒng)計(jì)圖;
(3)根據(jù)抽樣調(diào)查的結(jié)果,估算該校1000名學(xué)生中大約有多少人選擇“小組合作學(xué)習(xí)”?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為積極響應(yīng)“京津冀生態(tài)建設(shè)協(xié)同發(fā)展”,我區(qū)某街道要增大綠化面積,決定從備選的五種樹(shù)中選一種進(jìn)行栽種.為了更好的了解民意,工作人員在街道轄區(qū)范圍內(nèi)隨機(jī)走訪(fǎng)了部分居民,進(jìn)行“我最喜歡的一種樹(shù)”的調(diào)查活動(dòng)(每人選其中一種樹(shù)),將調(diào)查結(jié)果整理后,繪制出下面兩個(gè)不完整的統(tǒng)計(jì)圖.


請(qǐng)根據(jù)所給信息回答問(wèn)題:
(1)這次參與調(diào)查的居民人數(shù)為________;
(2)將條形統(tǒng)計(jì)圖補(bǔ)充完整;
(3)扇形統(tǒng)計(jì)圖中,![]() ________;“白蠟”所在扇形的圓心角度數(shù)為________;
________;“白蠟”所在扇形的圓心角度數(shù)為________;
(4)已知該街道轄區(qū)內(nèi)現(xiàn)在居民8萬(wàn)人,請(qǐng)你估計(jì)這8萬(wàn)人中最喜歡“銀杏”的有多少人?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com